Cho tam giác ABC nội tiếp đường tròn tâm O và AB<AC . Vẽ AH vuông góc với BC tại H . đường tròn đường kính AH lần lượt cắt AB ,AC tại I và K . Chứng minh ba đường thẳng AD , IK và BC đông qui
giúp em vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 3 2023
Bổ sung: ΔABC cân tại A
ΔABC cân tại A
=>AO đi qua trug diểm I của EF
Vẽ IK vuông góc AB tại K, gọi H và G lần lượt là giao của OA với BC và(O)
Vì OE vuông góc AB, IK vuông goc AB, GB vuông góc AB
=>OE//IK//GB
ΔABG có IK//GB
nên IK/BG=AI/AG
=>IK=AI*BG/AG
ΔABH có EI//BH
ΔABE có OE//BG
=>IH/AH=BE/BA=OG/AG và AE/AB=AI/AH
=>IH=AH*OE/AE
ΔABG có OE//BG
nên AB/AE=BG/OE
AH/AI=AB/AE=BG/OE
=>AH*OE=AI*BG
=>AH*OG=AI*BG
=>IK=IH
=>ĐPCM
29 tháng 11 2023
a: CD//AB
=>\(\widehat{CDB}=\widehat{ABC}\)
Xét (O) có
\(\widehat{DBC}\) là góc tạo bởi dây cung BC và tiếp tuyến BD
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{DBC}=\widehat{BAC}\)
Xét ΔDBC và ΔCAB có
\(\widehat{DBC}=\widehat{CAB}\)
\(\widehat{DCB}=\widehat{ABC}\)
Do đó: ΔDBC đồng dạng với ΔCAB
=>\(\dfrac{DC}{CB}=\dfrac{BC}{AB}\)
=>\(BC^2=AB\cdot DC\)
16 tháng 2 2023
DE//xx'
=>góc AED=góc EAx'=góc x'AC=góc ABC
Xét ΔAED và ΔABC có
góc AED=góc ABC
góc DAE chung
=>ΔAED đồng dạng vơi ΔABC
=>AE/AB=AD/AC
=>AE*AC=AB*AD
CM
8 tháng 3 2019
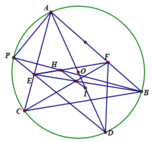
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.
11 tháng 8 2021
a) Ta có: ΔABC cân tại A
mà AH là đường cao ứng với cạnh BC
nên AH là đường trung tuyến ứng với cạnh BC
Ta có: AB=AC
nên A nằm trên đường trung trực của BC\(\left(1\right)\)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC\(\left(2\right)\)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(3)
Từ (1), \(\left(2\right),\left(3\right)\) suy ra A,O,H thẳng hàng
\(\Leftrightarrow A,O,H,D\) thẳng hàng
hay AD là đường kính của \(\left(O\right)\)