Tính giá trị biểu thức A = 2 + 5 + 8 ...+ 102
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


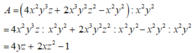
Giá trị biểu thức tại x = -2; y = 102; z= 102 là:
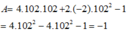
Chọn đáp án D

B=2-4+6-8+...+98-100+102
=(2-4)+(6-8)+...+(98-100)+102
=(-2)+(-2)+...+(-2)+102
=(-2).[(100-2):2+1]:2+102
=(-2).25+102
=(-50)+102=52
B = 2 - 4 + 6 - ... - 100 + 102
= -2 + -2 + ... + -2 + 102
= -2 x 25 + 102 ( Vì từ 2 đến 100 gồm ( 100 - 2 ) : 2 + 1 = 50 số chia thành 25 cặp số )
= -50 + 102
= 52

Vì y = 2 nên thay 2 vào vị trí của y trong phép tính ta có:
(–102) + y = (–102) + 2 = – (102 – 2) = –100.

Bài 1 :
\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)
hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)
mà \(xyz=2\Rightarrow-xyz=-2\)
hay N nhận giá trị -2
Bài 2 :
\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)
hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)
hay biểu thức trên nhận giá trị là 24
c, Ta có : \(a-b=3\Rightarrow a=3+b\)
hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)
\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi
1.Ta có:\(x+y+z=0\)
\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)
\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)
2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)
Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)
Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)
Vậy....

Đề thấy sai sai. Vì 102 - 2 = 100 không chia hết cho 3
=1820
k em nha em mới lớp 4 à