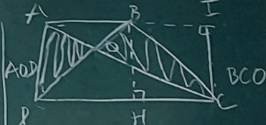
Cho hình thang abcd , có 2 đáy là AB và CD ( đáy lớn CD dài gấp 2 lần đáy nhỏ AB ). 2 đường chéo AC và BD cắt nhau tại O.
a) Hãy so sánh DT của 2 tam giác ABC và BCD
b) Hãy chứng tỏ DT của tam giác AOD = DT tam giác BOC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 1 2016
a) 2 tam giác ABC và BCD có cùng đường cao là đường cao = đương cao hình thang đáy DC = 2AB --> diện tich BCD gấp đôi
b) dễ dàng cm được diện tích tam giác diện tích tam giác ADC = BDC chúng có phần chung DOC còn lại phần riêng AOD = BOC
15 tháng 7 2020
a) Xét \(\Delta\)DAB có đáy AB và \(\Delta\)BDC có đáy DC lần lượt có đường cao hạ từ D và B ; 2 đường cao ấy bằng nhau
mà AB = 1/2 CD
=> S ( DAB ) = 1/2 x S( BDC)
=> 25 = 1/2 x S ( BDC) => S( BDC) = 50 ( cm^2)
=> S( ABCD ) = S(DAB ) + S( BDC) = 25 + 50 = 75 ( cm^2)
b) S( DAB ) = S( CAB ) vì có đường cao hạ từ C và D bằng nhau ; có chung đáy AB
=> S( DAO ) + S( OAB) = S( OAB ) + S(COB )
=> S( DAO ) = S ( COB)