rút gọn biểu thức (x2 - 1) / (x + 1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 11 2017
( x 2 + 1 ) ( x − 3 ) − ( x − 3 ) ( x 2 − 1 ) = ( x – 3 ) x 2 + 1 – x 2 – 1 = 2 ( x – 3 )
QT
1
19 tháng 9 2023
(x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
= (x – 2). [(2x3 – x2 + 1) + x2(1 – 2x)]
= (x – 2). [2x3 – x2 + 1 + x2 . 1 + x2 . (-2x)]
= (x – 2) . (2x3 – x2 + 1 + x2 – 2x3)
= (x – 2) .1
= x – 2
LG
1
18 tháng 7 2021
(x + 1) (x2 - x + 1) - (x -1) (x2 + x + 1)
= x3 + 1 - (x3 - 1) ( áp dụng hằng đẳng thức số 6 và 7 )
= x3 + 1 - x3 + 1
= 2
PT
1
CM
18 tháng 4 2017
x(2 x 2 – 3) – x 2 (5x + 1) + x 2
= x. 2 x 2 + x.(- 3) – ( x 2 . 5x + x 2 .1) + x 2
= (2 x 3 – 3x) – (5 x 3 + x 2 ) + x 2
= 2 x 3 – 3x – 5 x 3 – x 2 + x 2
= -3x – 3 x 3
PT
1
PT
1
CM
17 tháng 12 2017
1/2 x 2 (6x – 3) – x( x 2 + 1/2) + 1/2.(x + 4)
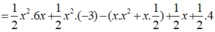
= (3 x 3 – 3/2. x 2 ) – ( x 3 + 1/2.x) + (1/2.x + 2)
= 3 x 3 - 3/2 x 2 – x 3 - 1/2 x + 1/2 x + 2
= ( 3 x 3 – x 3 ) - 3/2. x 2 – (1/2 x - 1/2 x) + 2
= 2 x 3 - 3/2 x 2 + 2
PT
1
PT
1
24 tháng 10 2021
\(\left(x-1\right)^2-\left(x+2\right)\left(x-2\right)\)
\(=x^2-2x+1-x^2+4\)
=-2x+5
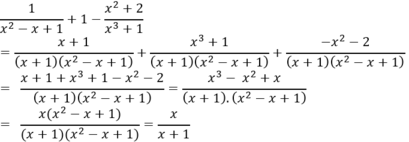
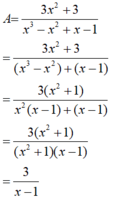
(x2 - 1) / (x + 1)
=(x-1)(x+1)/x+1
=x-1
\(\frac{x^2-1}{x+1}=\frac{x^2+x-x-1}{x+1}=\frac{x.\left(x+1\right)}{x+1}-\frac{x+1-2}{x+1}=x-\frac{x+1}{x+1}+\frac{2}{x+1}=x-1+\frac{2}{x+1}\)