cho a, b, c là độ dài 3 cạnh của tam giác. Chứng minh ab+ac+bc <= a2+b2+c2 < 2 (ab+ac+bc)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Vì a, b, c là độ dài 3 cạnh của một tam giác
⇒ a + c > b và a + b > c (Bất đẳng thức tam giác)
⇒ a + c – b > 0 và a + b – c > 0
Ta có: (b – c)2 < a2
⇔ a2 – (b – c)2 > 0
⇔ (a – (b – c))(a + (b – c)) > 0
⇔ (a – b + c).(a + b – c) > 0 (Luôn đúng vì a + c – b > 0 và a + b – c > 0).
Vậy ta có (b – c)2 < a2 (1) (đpcm)
b) Chứng minh tương tự phần a) ta có :
( a – b)2 < c2 (2)
(c – a)2 < b2 (3)
Cộng ba bất đẳng thức (1), (2), (3) ta có:
(b – c)2 + (c – a)2 + (a – b)2 < a2 + b2 + c2
⇒ b2 – 2bc + c2 + c2 – 2ca + a2 + a2 – 2ab + b2 < a2 + b2 + c2
⇒ 2(a2 + b2 + c2) – 2(ab + bc + ca) < a2 + b2 + c2
⇒ a2 + b2 + c2 < 2(ab + bc + ca) (đpcm).

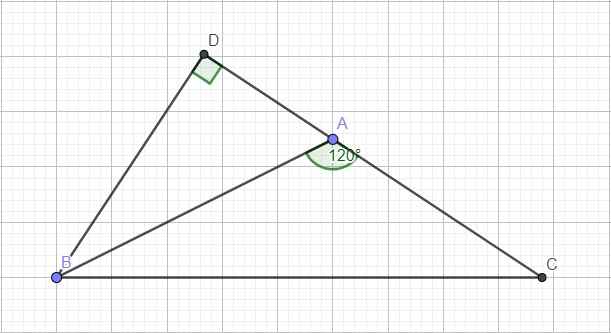
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)

Ta có:
a<b+ca<b+c
--> a+a<a+b+ca+a<a+b+c
--> 2a<22a<2
--> a<1a<1
Tương tự ta có : b<1,c<1b<1,c<1
Suy ra: (1−a)(1−b)(1−c)>0(1−a)(1−b)(1−c)>0
⇔ (1–b–a+ab)(1–c)>0(1–b–a+ab)(1–c)>0
⇔ 1–c–b+bc–a+ac+ab–abc>01–c–b+bc–a+ac+ab–abc>0
⇔ 1–(a+b+c)+ab+bc+ca>abc1–(a+b+c)+ab+bc+ca>abc
Nên abc<−1+ab+bc+caabc<−1+ab+bc+ca
⇔ 2abc<−2+2ab+2bc+2ca2abc<−2+2ab+2bc+2ca
⇔ a2+b2+c2+2abc<a2+b2+c2–2+2ab+2bc+2caa2+b2+c2+2abc<a2+b2+c2–2+2ab+2bc+2ca
⇔ a2+b2+c2+2abc<(a+b+c)2−2a2+b2+c2+2abc<(a+b+c)2−2
⇔ a2+b2+c2+2abc<22−2a2+b2+c2+2abc<22−2 , (do a+b=c=2a+b=c=2 )
⇔ dpcm

** Lần sau bạn lưu ý viết đề bằng công thức toán (hộp công thức nằm ở nút biểu tượng $\sum$ bên trái khung soạn thảo)
Lời giải:
a) Vì $a,b,c$ là độ dài 3 cạnh tam giác nên theo BĐT tam giác ta có:
$c< a+b\Rightarrow c^2< c(a+b)$
$b< a+c\Rightarrow b^2< b(a+c)$
$a<b+c\Rightarrow a^2< a(b+c)$
$\Rightarrow a^2+b^2+c^2< c(a+b)+b(a+c)+a(b+c)$
hay $a^2+b^2+c^2< 2(ab+bc+ac)$ (đpcm)
b)
Áp dụng BĐT Bunhiacopxky:
$\text{VT}[a(b+c-a)+b(a+c-b)+c(a+b-c)]\geq (a+b+c)^2$
$\text{VT}[2(ab+bc+ac)-(a^2+b^2+c^2)]\geq (a+b+c)^2$
$\Rightarrow \text{VT}\geq \frac{(a+b+c)^2}{2(ab+bc+ac)-(a^2+b^2+c^2)}(*)$
Mà theo BĐT Cô-si:
$a^2+b^2+c^2\geq ab+bc+ac\Rightarrow a^2+b^2+c^2\geq \frac{(a+b+c)^2}{3}$. Do đó:
$2(ab+bc+ac)-(a^2+b^2+c^2)=(a+b+c)^2-2(a^2+b^2+c^2)$
$\leq (a+b+c)^2-2.\frac{(a+b+c)^2}{3}=\frac{(a+b+c)^2}{3}(**)$
Từ $(*); (**)\Rightarrow \text{VT}\geq 3$ (đpcm)
Dấu "=" xảy ra khi $x=y=z$
Lời giải khác của câu b
Đặt $b+c-a=x; a+c-b=y; a+b-c=z$. Theo BĐT tam giác thì $x,y,z>0$
$\Rightarrow c=\frac{x+y}{2}; a=\frac{y+z}{2}; b=\frac{x+z}{2}$
Bài toán trở thành:
Cho $x,y,z>0$. CMR $\frac{y+z}{2x}+\frac{z+x}{2y}+\frac{x+y}{2z}\geq 3$
Thật vậy:
Áp dụng BĐT Cô-si:
\(\frac{y+z}{2x}+\frac{z+x}{2y}+\frac{x+y}{2z}\geq 3\sqrt[3]{\frac{(x+y)(y+z)(x+z)}{8xyz}}\geq 3\sqrt[3]{\frac{2\sqrt{xy}.2\sqrt{yz}.2\sqrt{xz}}{8xyz}}=3\)
Ta có đpcm
Dấu "=" xảy ra khi $x=y=z$ hay $a=b=c$
Ta có (a+b)2 >=0 => a2 + 2ab + b2 >= 0 => a2 + b2 >= 2ab. (1)
(b+c)2 >=0 => b2 + 2bc + c2 >= 0 => b2 + c2 >= 2bc. (2)
(c+a)2 >=0 => c2 + 2ca + a2 >= 0 => c2 + a2 >= 2ca. (3)
Cộng (1), (2), (3), theo vế ta có 2(a2 + b2 + c2)>=2(ab+bc+ca)
suy ra a2 + b2 + c2>=ab+bc+ca (*)
Áp dụng bất đẳng thức trong tam giác ta có:
a+b>c => ac+bc>c2. (4)
b+c>a => ab+ac>a2. (5)
c+a>b => bc+ab>b2. (6)
Cộng (4), (5), (6) theo vế ta có 2(ab+bc+ca)>a2+b2+c2(**)
Từ (*) và (**) suy ra đpcm.
xfffff