so sánh 2 số 2017:2018 và 2018:2019
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AK
10 tháng 4 2018
Ta có :
\(\frac{2016}{2017}>\frac{2016}{2017+2018+2019}\)
\(\frac{2017}{2018}>\frac{2017}{2017+2018+2019}\)
\(\frac{2018}{2019}>\frac{2018}{2017+2018+2019}\)
\(\Rightarrow\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}>\) \(\frac{2016}{2017+2018+2019}+\frac{2017}{2017+2018+2019}+\frac{2018}{2017+2018+2019}\)
\(\Rightarrow P>\frac{2016+2017+2018}{2017+2018+2019}\)
\(\Rightarrow P>Q\)
Chúc bạn học tốt !!!
10 tháng 4 2018
vì P có các số bé hơn 1 còn Q có các số lớn hơn 1 =>P<Q
Vậy P<Q.
mình làm hơi tắt xin bạn thông cảm bạn tự viết các số có trong P;Q ra nhá
ET
1
H
12 tháng 4 2018
Ta có : \(0< \frac{2017}{2018}< 1\) nên \(\frac{2017}{2018}>\frac{2017+2019}{2018+2019}\)(1)
\(0< \frac{2018}{2019}< 1\) nên \(\frac{2018}{2019}>\frac{2018+2018}{2018+2019}\) (2)
Cộng vế theo vế 1 và 2 ta được : \(B=\frac{2017}{2018}+\frac{2018}{2019}>\frac{2017+2018+2018+2019}{2018+2019}=\frac{2017+2018}{2018 +2019}+1=A+1>A\)
Vậy B>A
LT
5
12 tháng 4 2018
Ta có :
\(A=\frac{2017+2018}{2018+2019}=\frac{2017}{2018+2019}+\frac{2018}{2018+2019}\)
Vì :
\(\frac{2017}{2018+2019}< \frac{2017}{2018}\)
\(\frac{2018}{2018+2019}< \frac{2018}{2019}\)
Nên \(\frac{2017}{2018+2019}+\frac{2018}{2018+2019}< \frac{2017}{2018}+\frac{2018}{2019}\) ( cộng theo vế )
\(\Rightarrow\)\(A< B\)
Vậy \(A< B\)
Chúc bạn học tốt ~
T1
12 tháng 4 2018
Mình thấy là A<B.
Tách A=2017+2018/2018+2019=2017/2018+2019 + 2018/2018+2019
Ta thấy từng số hạng của A lần lượt nhỏ hơn số hạng của B
=> A<B
NM
1
T
8 tháng 6 2019
#)Giải :
\(Q=2+\frac{2016}{2017+2018+2019}+\frac{2017}{2017+2018+2019}+\frac{2018}{2017+2018+2019}\)
Ta thấy : \(2>\frac{2016}{2017};2>\frac{2017}{2018};2>\frac{2018}{2019}\left(1\right)\)
\(\frac{2016}{2017+2018+2019}< \frac{2016}{2017}\left(2\right)\)
\(\frac{2017}{2017+2018+2019}< \frac{2017}{2018}\left(3\right)\)
\(\frac{2018}{2017+2018+2019}< \frac{2018}{2019}\left(4\right)\)
Từ (1) (2) (3) (4) \(\Rightarrow P>Q\)
6 tháng 4 2023
`a,`
`5/6=1-1/6`
`7/8=1-1/8`
Mà `1/6>1/8 -> 5/6<7/8`
`b,`
`9/5=(9 \times 2)/(5 \times 2)=18/10`
`3/2=(3 \times 5)/(2 \times 5)=15/10`
`18/10 > 15/10 -> 9/5 > 3/2`
`c,`
`2017/2018 = 1-1/2018`
`2019/2020=1-1/2020`
`1/2018 > 1/2020 -> 2017/2018 < 2019/2020`
`d,`
`2018/2017 = 1+1/2017`
`2020/2019 = 1+1/2019`
`1/2017 > 1/2019 -> 2018/2017>2020/2019`
NT
1
Ta có:
=1-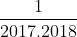
vì 2017.2018>2018.2019
=>
> 
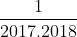=> 1-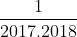
> 
=> A>B
dài thế