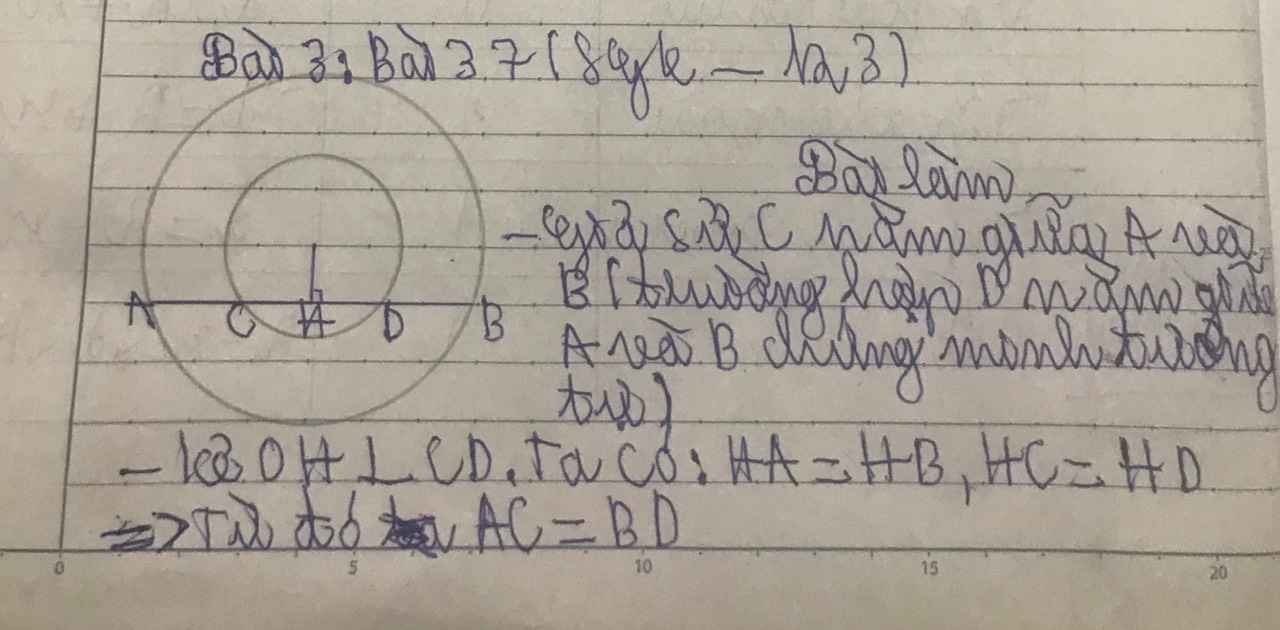Câu 3: Trang 131 sách VNEN 9 tập 1 Cho hai đường tròn (O; R) và (O'; R') cắt nhau tại A và B (R > R'). Gọi M là trung điểm của OO'. Kẻ đường thẳng vuông góc với MA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; R') theo thứ tự tại C và D (khác A). a) Chứng minh rằng AC = AD. b) Lấy K sao cho M là trung điểm của AK. Chứng minh rằng KB vuông góc với AB. c) Kẻ đường kính AE của đường tròn (O) và đường kính AF của (O'). Chứng minh rằng bốn điểm E, K, B, F thẳng hàng và OO' song song với EF. d) Chứng minh K là trung điểm của EF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ơi, mik nhìn cái đề mà ko muốn đọc. Đọc xong rồi lại chả hiểu đề nó muốn nói gì. Bạn nên trình bày sao cho hợp lí và dễ hiểu, chứ nhìn như 1 mớ hỗn độn như thế này thì ai mà hiểu? Chưa kể hình thì ko có thì làm sao mà trả lời?





- Đơn thứ nhất:
+ Thiếu quốc hiệu, tiêu ngữ.
+ Thiếu mục nêu tên người gửi.
+ Thiếu địa ddiemr, thời gian viết đơn.
+ Thiếu chữ kí của người viết đơn.
- Đơn thứ hai:
+ Quốc hiệu viết thường.
+ Thiếu địa điểm, thời gian làm đơn.
+ Thiếu tên, lớp.
+ Thiếu chữ kí
Cách sửa: bổ xung những mục còn thiếu vào đơn để hoàn chỉnh.

| nội dung | lãnh địa phong kiến | thành thị trung đại |
| thời gian xuất hiện | cuối tk V | cuối tk XI |
| tp dân cư chủ yếu | LÃNH CHÚA và NÔNG NÔ | thợ thủ công và thương nhân |
| hdkt chủ yếu | tự cung tự cấp | trao đổi buôn bán |

Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.