Một vật có khối lượng m = 3 kg nằm yên trên sàn nhà. Dưới tác dụng của hợp lực Fhl theo phương ngang và có độ lớn không đổi Fhl = 1,8 N, vật chuyển động thẳng nhanh dần đều. 1. Hãy tính: a) Gia tốc của vật ? b) Vận tốc và độ dịch chuyển khi vật chuyển động được 6 giây ? 2. Sau khoảng thời gian trên lực kéo ngừng tác dụng, vật chuyển động thẳng chậm dần đều và dừng lại. Biết khoảng thời gian từ lúc vật chuyển động thẳng chậm dần đều và dừng lại là 4 giây. a) Tính độ dịch chuyển của vật trong khoảng thời gian trên ? b) Tính độ lớn của lực cản tác dụng lên vật ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định luật ll Niuton: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
Độ lớn lực kéo:
\(F=m.a+F_{ms}=m.a+\mu mg=50\cdot0,5+0,1\cdot50\cdot10=75N\)

a)\(v=54km/h=15m/s\)
Gia tốc của vật: \(v^2-v_0^2=2aS\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2S}=\dfrac{15^2-0^2}{2\cdot112,5}=1m/s^2\)
b)Theo định luật ll Niuton: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\Rightarrow F_{ms}=F-m.a=12-3\cdot1=9N\)
Hệ số ma sát: \(F_{ms}=\mu mg\)
\(\Rightarrow\mu=\dfrac{F_{ms}}{m\cdot g}=\dfrac{9}{3\cdot10}=0,3\)

Định luật ll Niu-tơn ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
\(\Rightarrow F=F_{ms}+m\cdot a=6+3\cdot2=12N\)

a, Gia tốc của vật \(a=\dfrac{2s}{t^2}=\dfrac{2.24}{4^2}=3\left(m/s^2\right)\)
Lực kéo \(F=m.a=2.3=6N\)
b, Sau 4s, vận tốc của vật \(v=v_0+at=3.4=12\left(m/s\right)\)
\(F_{mst}=-m.a\Leftrightarrow\mu_t.m.g=-m.a\Rightarrow a=-\mu_t.g=-0,2.10=-2\left(m/s^2\right)\)
Thời gian để vật dừng lại \(t=\dfrac{v-v_0}{a}=\dfrac{-12}{-2}=6s\)
a, Gia tốc của vật a=2st2=2.2442=3(m/s2)a=2st2=2.2442=3(m/s2)
Lực kéo F=m.a=2.3=6NF=m.a=2.3=6N
b, Sau 4s, vận tốc của vật v=v0+at=3.4=12(m/s)v=v0+at=3.4=12(m/s)
Fmst=−m.a⇔μt.m.g=−m.a⇒a=−μt.g=−0,2.10=−2(m/s2)Fmst=−m.a⇔μt.m.g=−m.a⇒a=−μt.g=−0,2.10=−2(m/s2)
Thời gian để vật dừng lại t=v−v0a=−12−2=6s

Định luật ll Niu tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F\cdot F_{ms}=m\cdot a\)
\(\Rightarrow F=m\cdot a+F_{ms}=m\cdot a+\mu mg=3\cdot2+0,2\cdot3\cdot10=12N\)
Nếu bỏ qua ma sát quãng đường vật đi đc là:
\(S=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot2\cdot2^2=4m\)

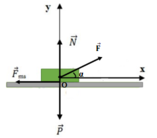
a) Các lực tác dụng lên vật được biểu diễn như hình vẽ. Chọn hệ trục Ox theo hướng chuyển động, Oy vuông góc phương chuyển động.
Áp dụng định luật II Niu – tơn ta được:
![]()
Chiếu hệ thức vecto lên trục Ox ta được:
Fcosα - Fms = ma (1)
Chiếu hệ thức vecto lên trục Oy ta được:
Fsinα - P + N = 0 ⇔ N = P - Fsinα (2)
Mặt khác Fms = μtN = μt(P - Fsinα) (3)
Từ (1) và (2) (3) suy ra:
![]()
b) Để vật chuyển động thẳng đều (a = 0) ta có:
![]()
⇔ Fcosα - μt(P - Fsinα) ⇒ F = 12(N)

a. Gia tốc của vật:
\(a=\dfrac{F_{hl}}{m}=\dfrac{1,8}{3}=0,6\left(\dfrac{m}{s^2}\right)\)
b. Vận tốc của vật sau 6s là:
\(v=v_0+at=0,6.6=3,6\left(\dfrac{m}{s}\right)\)
Độ dịch chuyển khi vật chuyển động được 6s là:
\(s=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,6.6^2=10,8\left(m\right)\)
c. Gia tốc của vật là: \(a'=\dfrac{v-v_0}{t}=\dfrac{0-3,6}{4}=-0,9\left(\dfrac{m}{s^2}\right)\)
Độ dịch chuyển của vật trong thời gian trên là:
\(s=\dfrac{1}{2}at^2=\dfrac{1}{2}0,9.4^2=7,2\left(m\right)\)
d. Độ lớn lực cản tác dụng lên vật là:
\(F_c=ma=0,9.3=2,7\left(N\right)\)