Cho A =0,1(2453) là 1 số thập phân vô hạn tuần hoàn. Tìm số k nguyên dương nhỏ nhất để kA là một số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 1 2019
- Ta có:
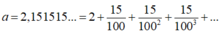
- Vì:
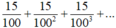
là tổng của cấp số nhân lùi vô hạn với số hạng đầu.
,
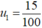công bội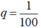 
nên
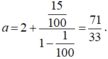
Do đó m+n=71+33=104
Chọn A
CM
28 tháng 5 2017
Đáp án C
Ta có:
0 , 32111 . . . = 32 100 + 1 10 3 + 1 10 4 + 1 10 5 + . . . = 32 100 + 1 10 3 1 - 1 10 = 289 900 .
Vậy a = 289 , b = 900 . Do đó a - b = 289 - 900 = - 611 .
CM
4 tháng 9 2018
- Ta có:
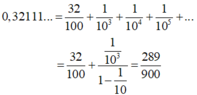
- Vậy a = 289, b = 900.
- Do đó: a - b = 289 – 900 = - 611.
Chọn B.
16 tháng 10 2016
Ta có: \(n\left(n+1\right)\left(n+2\right)\) chia hết cho 3.
=> \(\frac{52}{n\left(n+1\right)\left(n+2\right)}\) là stp hữu hạn.
16 tháng 10 2016
Ta thấy: n(n + 1)(n + 2) là tích 3 số tự nhiên liên tiếp nên n(n + 1)(n + 2) chia hết cho 3
Mà 52 không chia hết cho 3
Như vậy, đến khi tối giản, mẫu số của phân số \(\frac{52}{n\left(n+1\right)\left(n+2\right)}\) có ước là 3, khác 2 và 5
Do đó, \(\frac{52}{n\left(n+1\right)\left(n+2\right)}\) có thể viết được dưới dạng số thập phân vô hạn tuần hoàn
Lời giải:
$A=0,1+0,0(2453)=\frac{1}{10}+\frac{2453}{99990}=\frac{566}{4545}$ (đây đã là dạng tối giản)
Vậy số nguyên k nguyên dương nhỏ nhất để $kA$ nguyên là $4545$