Một hằng số quan trọng trong toán học là số $e$ có giá trị gần đúng với $12$ chữ số thập phân là $2,718281828459$.
a) Giả sử ta lấy giá trị $2,7$ làm giá trị gần đúng của $e$. Hãy chứng tỏ sai số tuyệt đối không vượt quá $0,02$ và sai số tương đối không vượt quá $0,75 \%$.
b) Hãy quy tròn $e$ đến hàng phần nghìn.
c) Tìm số gần đúng của số $e$ với độ chính xác $0,00002$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Sai số tuyệt đối là: \(\Delta = \left| {e - 2,7} \right| = \;|2,718281828459 - 2,7|\; = 0,018281828459 < 0,02\)
Sai số tương đối là: \({\delta _a} = \frac{{{\Delta _a}}}{{|a|}} < \frac{{0,02}}{{2,7}} \approx 0,74\% \)
b) Quy tròn e đến hàng phần nghìn ta được: 2,718.
c)
Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,00002 là hàng phần trăm nghìn.
Quy tròn e đền hàng phầm trăm nghìn ta được 2,71828

a) Xét: | π - 3,14 | = π - 3,14 < 3,1416 - 3,14 = 0,0016 < 0,002
b) |π - 3,1416 I = 3,1416 - π < 3,1416 - 3,1415 = 0,0001
Chúc bạn học tốt ~
a) Xét: | π - 3,14 |
= π - 3,14 < 3,1416 - 3,14 = 0,0016 < 0,002
b) |π - 3,1416 I = 3,1416 - π < 3,1416 - 3,1415
= 0,0001

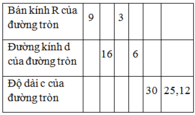
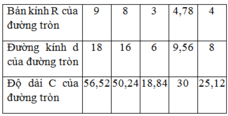
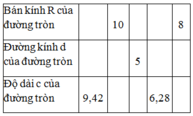
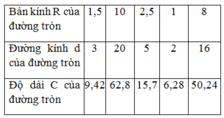
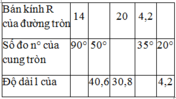
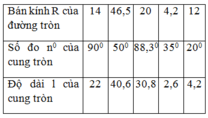
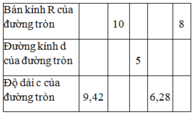
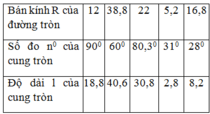
Áp dụng công thức:l= πRn/180.
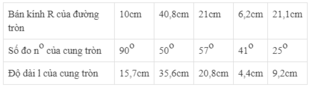
+ Độ dài cung n0 của đường tròn bán kính R là :Kiến thức áp dụng
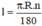

a) Dùng phân số \(\frac{{22}}{7}\) để xấp xỉ cho \(\pi \) tức là \(\pi \)là số đúng, \(\frac{{22}}{7}\) là số gần đúng.
b) Ta có: \(3,1415 < \pi < 3,1416\)
\(\begin{array}{l} \Rightarrow \frac{{22}}{7} - 3,1415 > \frac{{22}}{7} - \pi > \frac{{22}}{7} - 3,1416\\ \Leftrightarrow 0,001357 > \frac{{22}}{7} - \pi > 0,001257\\ \Rightarrow \Delta = \left| {\frac{{22}}{7} - \pi } \right| < 0,001357\end{array}\)
Vậy sai số tuyệt đối không quá \(0,001357\)
Sai số tương đối là \(\delta = \frac{\Delta }{{\frac{{22}}{7}}} < \frac{{0,001357}}{{\frac{{22}}{7}}} \approx 0,03\% \)

Ta có 16 , 25 = 16 + 0 , 25 .
Xét hàm số f x = x ⇒ f ' x = 1 2 x
Chọn x0 = 16 và ∆ x = 0,25 , ta có f x 0 + Δ x ≈ f x 0 + f ' x 0 . Δ x
⇒ 16 + 0 , 25 ≈ 16 + 1 2 16 .0 , 25 = 4 + 0 , 03125 = 4 , 03125 ⇒ 16 + 0 , 25 ≈ 4 , 0313
Chọn đáp án A.
a) Sai số tuyệt đối ∆ = |2,718281828459 – 2,7| = 0,018281828459 < 0,02.
Sai số tương đối
δ=Δ|2,7|=0,0182818284592,7≈0,68%< 0,75%.
b) Quy tròn e đến hàng phần nghìn ta được số gần đúng là 2,718.
c) Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác d = 0,00002 là hàng phần trăm nghìn. Quy tròn e đến hàng phần trăm nghìn ta được số gần đúng của e là 2,71828.
a) Sai số tuyệt đối ∆ = |2,718281828459 – 2,7| = 0,018281828459 < 0,02.
Sai số tương đối
δ=Δ:|2,7|=0,018281828459 : 2,7≈
0,68% < 0,75%.
b) Quy tròn e đến hàng phần nghìn ta được số gần đúng là 2,718.
c) Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác d = 0,00002 là hàng phần trăm nghìn. Quy tròn e đến hàng phần trăm nghìn ta được số gần đúng của e là 2,71828.