Câu hỏi : Cho đường thẳng c cắt a và b sao cho một cặp góc so le trong bằng nhau. Đường thẳng d vuông góc với đường thẳng a.
a) Vẽ hình ghi giả thuyết, kết luận.
b) Hỏi d có vuông góc với b không? Vì sao?
Giúp e ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2017
a) Ta có :
c // p \(\Leftrightarrow\hept{\begin{cases}a⊥b\\b⊥p\\a\backslash\backslash c\end{cases}}\)
Vậy c // p ( dựa theo mối quan hệ giữa vuông góc và song song )
b)GT : a cắt b tại A ; b // c
KL : a cắt c
15 tháng 8 2017
a, C và P có quan hệ Vuông GÓC vì a vuông góc với b, b vuông góc với p
=> a và p song song ( Định Lý) (1)
Mà a song song với c (2)
Từ (1) và (2)=>c song song với p
b,
giả thiết: có 2 đường thẳng song song
1 đường thẳng cắt 1 trong 2 đường thẳng song song đó
Kết luận: đường thẳng cắt 1 trong 2 đường thẳng trên thì nó cắt đường thẳng còn lại
CHÚC BN HỌC TỐT!!!!!!!!!
NHỚ K ĐÚNG CHO MÌNH NHA
10 tháng 11 2021
Tham khảo!
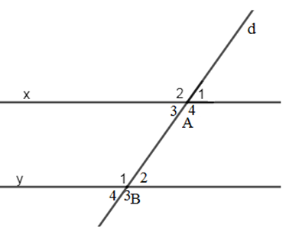
Giả thiết: Đường thẳng cắt hai đường thẳng sao cho có một góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
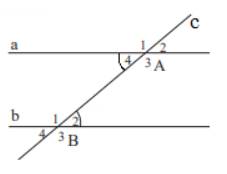
Vì đường thẳng c cắt hai đường thẳng a và b tạo thành một cặp góc so le trong ( góc A4 và B3) bằng nhau nên a // b ( Dấu hiệu nhận biết 2 đường thẳng song song)
Vì a // b nên theo tính chất của 2 đường thẳng song song:
a) Các so le trong bằng nhau
b) Các góc đồng vị bằng nhau
16 tháng 6 2017
a)
b) A4 và B2 cũng là so le trong .
Vì A4 = 180 - A1
B2 = 180 - B3 ( tính chất 2 góc kề bù )
c) A1 = B3 => A4 = B2
d; e ) không bt lắm
29 tháng 9 2015
d vuông góc với hai đường thẳng còn lại vì bạn chép cái tính chất sgk ra là đc
b: c cắt a và b và tạo thành 1 cặp góc so le trong bằng nhau
nên a//b
mà d vuông góc a
nên d vuông góc b