Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các cạnh SA, BC. Trên cạnh AB lấy điểm K không trùng với trung điểm của AB. Tìm thiết diện của hình chóp S.ABC và (MNK)?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
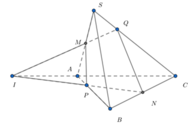
Phương pháp : Dựng điểm Q và áp dụng định lý Menenaus.
Cách giải : Gọi I là giao điểm của PN và AC. Suy ra Q là giao điểm của IM và SC.
Áp dụng định lý Menenaus cho tam giác SAC ta có :
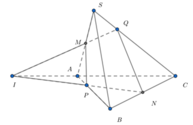

Chọn đáp án A
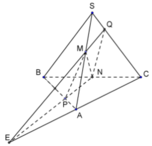
Trong mặt phẳng (ABC), gọi E = NP ∩ AC
Khi đó Q chính là giao điểm của SC với EM
Áp dụng định lý Menelaus vào tam giác ABC ta có:
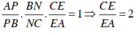
Áp dụng định lý Menelaus vào tam giác SAC ta có:
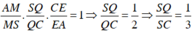


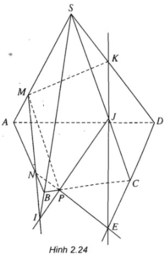
Gọi \(J=IP\cap SC\), ta có \(J=SC\cap\left(MNP\right)\)
Gọi \(E=NP\cap CD\), ta có \(E=CD\cap\left(MNP\right)\)
Gọi \(K=JE\cap SD\), ta có \(K=SD\cap\left(MNP\right)\)

a lần lượt tìm giao điểm của mặt phẳng (MNP) với các đường thẳng chứa các cạnh của hình chóp.
Gọi I = MN ∩ SB
Ta có:
Vậy I = SB ∩ (MNP).
Từ đó, làm tương tự ta tìm được giao điểm của (MNP) với các cạnh còn lại.
Cụ thể :
Gọi J = IP ∩ SC, ta có J = SC ∩ (MNP)
Gọi E = NP ∩ CD, ta có E = CD ∩ (MNP)
Gọi K = JE ∩ SD, ta có K = SD ∩ (MNP)

Đáp án A
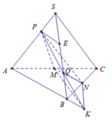
Gọi H là hình chiếu của S lên mặt đáy A B C suy ra S H ⊥ A B C thì H là trung điểm của AC.
Ta có:
S H = 9 − 2 = 7 ; K = P Q ∩ A B ; A B = A C = 2
Dựng P E / / A B ta có:
K B P E = Q B Q E = 1 ⇒ K B = P E = 1 3 A B = 2 3
S M N K = 1 2 d K ; M N . M N = 1 2 N B . M N = 1 2 d P ; A B C = 2 3 . S H = 2 3 7 ⇒ V P . M N K = 1 3 d P ; A B C . S M N K = 7 9
Lại có:
K Q K P = 1 2 ⇒ V Q . M N P V K . M N P = 1 2 ⇒ V Q . M N P = 1 2 V K . M N P = 7 18

Chọn đáp án B
Do S.ABCD là hình chóp tứ giác đều nên mỗi mặt bên là một tam giác cân tại đỉnh S.
Theo giả thiết ta có
![]()
Cắt hình chóp theo cạnh bên SA rồi trải các mặt bên thành một mặt phẳng ta được hình vẽ bên sao cho khí ghép lại thì A ≡ A '
Suy ra A S A ' ⏜ = 4 . A S B ⏜ = π 3 và ∆ S A A ' đều cạnh SA = a

Khi đó tổng AM + MN + NP + PQ là tổng của các đường gấp khúc.
Tổng này đạt nhỏ nhất bằng AQ nếu xảy ra trường hợp các điểm A, M, N, P, Q thẳng hàng.
Mà ∆ S A A ' đều có Q là trung điểm SA nên A Q = S A 3 2 = a 3 2
Vậy m i n A M + M N + N P + P Q = a 3 2
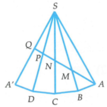
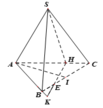
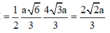
Thầy gợi ý cách xác định thiết diện thông qua hình vẽ sau:
Em kéo dài KN cắt AC tại P (trong mp(ABC)), từ đó tiếp tục dựng hình để xác định giao tuyến với các mặt còn lại của hình chóp để có thiết diện là tứ giác KMQN nhé