Question

[mặt trời xanh]

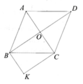
Gọi O là giao điểm của hai đường chéo AC, BD của hình thang ABCD với đáy lớn là CD. Các đường thẳng kẻ từ A, B song song với AC, BD cắt các đường chéo AC, BD tại E, F.

a) Chứng minh tứ giác ABFE là hình thang.

b) Chứng minh AB²=ÈF.CD

c) S₁,S₂,S₃,S₄ là diện tich các tam giác OAB, OCD, OAD VÀ OBC. Chứng minh S₁.S₂=S_3.S₄

d) đường thẳng qua O song song với AB cắt AD, BC tại M,N. Chứng minh 1/AB+1/CD=2/MN

Answer 1

[Phan Thanh Tịnh]

c)\(\Delta AOB,\Delta BOC\)có chung đường cao hạ từ B nên\(\frac{S_1}{S_4}=\frac{OA}{OC}\left(1\right)\)

\(\Delta AOD,\Delta DOC\)có chung đường cao hạ từ D nên\(\frac{S_3}{S_2}=\frac{OA}{OC}\left(2\right)\)

Từ (1) và (2),ta có\(\frac{S_1}{S_4}=\frac{S_3}{S_2}\Rightarrow S_1.S_2=S_3.S_4\)

d) Áp dụng hệ quả định lí Ta-lét,ta có :

\(\Delta ADB\)có OM // AB nên\(\frac{OM}{AB}=\frac{OD}{DB}\left(3\right)\)

\(\Delta ABC\)có ON // AB nên\(\frac{ON}{AB}=\frac{OC}{AC}\left(4\right);\frac{ON}{AB}=\frac{NC}{BC}\left(5\right)\)

\(\Delta COD\)có AB // CD nên\(\frac{OD}{DB}=\frac{OC}{AC}\left(6\right)\)

\(\Delta BDC\)có ON // DC nên\(\frac{ON}{CD}=\frac{BN}{NC}\left(7\right)\)

Từ (3),(5),(6),ta có\(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\Rightarrow MN=2ON\Rightarrow\frac{1}{ON}=\frac{2}{MN}\)

Cộng (5) và (7),vế theo vế,ta có :\(\frac{ON}{AB}+\frac{ON}{CD}=\frac{BN}{BC}+\frac{NC}{BC}\Leftrightarrow ON.\left(\frac{1}{AB}+\frac{1}{CD}\right)=1\Rightarrow\frac{1}{AB}+\frac{1}{CD}=\frac{1}{ON}=\frac{2}{MN}\)

P/S : Bạn xem lại đề để có thể xác định E,F nhé

Answer 2

[Minh Nguyễn]

chịu rùi tớ không biết !!!