Cho hàm số y=\(\dfrac{1}{2}x-3\) có đồ thị (d1) y= -2x + 3 có đồ thị (d2)
a) Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của (d1) và (d2) bằng phét toán
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tự vẽ
b, Hoành độ giao điểm thỏa mãn phương trình
\(2x+3=-x\Leftrightarrow3x=-3\Leftrightarrow x=-1\Rightarrow y=1\)
Vậy \(x=-1;y=1\)

b, PT hoành độ giao điểm là \(\dfrac{3}{2}x-2=-2x+5\Leftrightarrow\dfrac{7}{2}x=7\Leftrightarrow x=2\Leftrightarrow y=1\)
\(\Leftrightarrow A\left(2;1\right)\)
Vậy A(2;1) là tọa độ giao điểm 2 đths

b, PT hoành độ giao điểm là \(2x-1=-x+5\Leftrightarrow3x=6\Leftrightarrow x=2\Leftrightarrow y=3\)
\(\Leftrightarrow A\left(2;3\right)\)
Vậy A(2;3) là tọa độ giao điểm 2 đths

a: 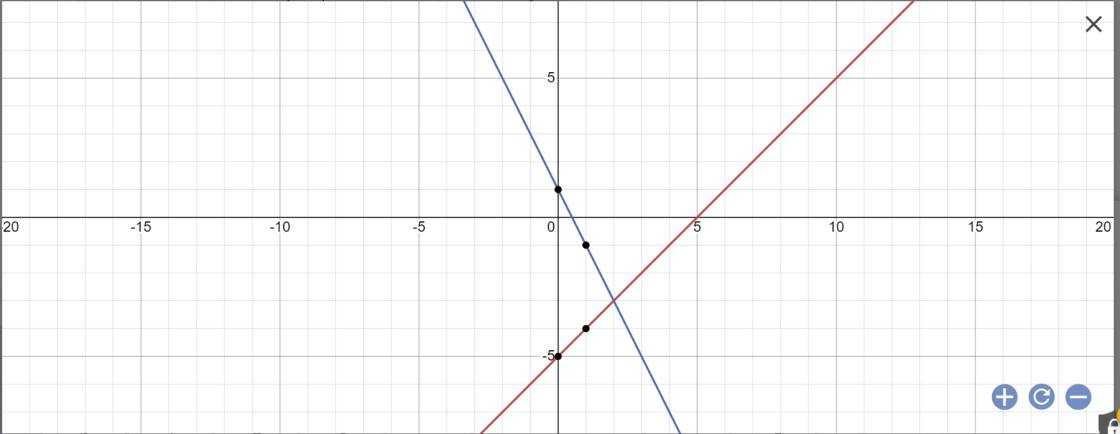
b: Phương trình hoành độ giao điểm là:
-2x+1=x-5
=>-2x-x=-5-1
=>-3x=-6
=>x=2
Thay x=2 vào y=x-5, ta được:
\(y=2-5=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
c: (d1): y=x-5
=>x-y-5=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)
(d2): y=-2x+1
=>y+2x-1=0
=>2x+y-1=0
Khoảng cách từ O đến (d2) là:
\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)

a:
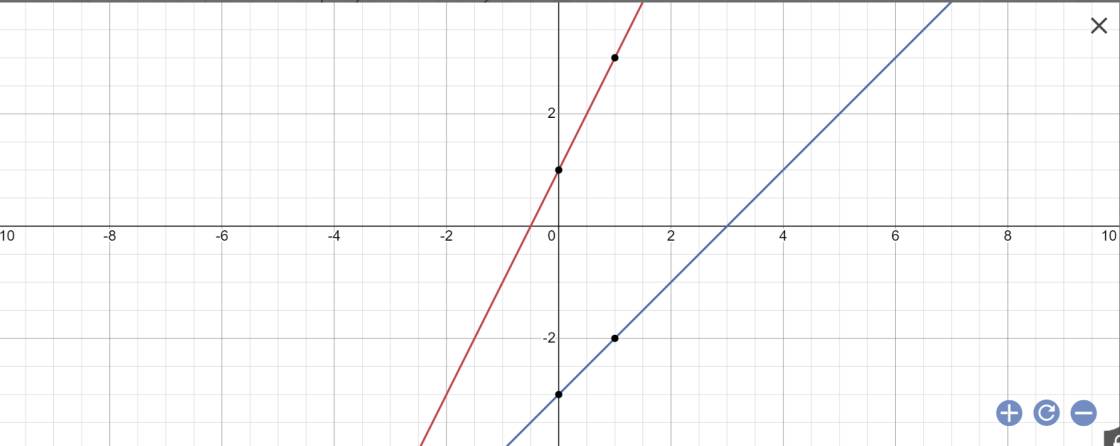
b: Phương trình hoành độ giao điểm là:
\(2x+1=x-3\)
=>\(2x-x=-3-1\)
=>x=-4
Thay x=-4 vào y=x-3, ta được:
\(y=-4-3=-7\)
Vậy: Tọa độ giao điểm của (D1) và (D2) là B(-4;-7)
c: Đặt phương trình đường thẳng (d3): y=ax+b
Vì (d3)//(d1) nên \(\left\{{}\begin{matrix}a=2\\b< >1\end{matrix}\right.\)
Vậy: y=2x+b
Thay x=1 và y=0 vào y=2x+b, ta được:
\(b+2\cdot1=0\)
=>b+2=0
=>b=-2
Vậy: (d): y=2x-2

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-5=\dfrac{1}{2}x\\y=2x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}x=5\\y=2x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=2\cdot\dfrac{10}{3}-5=\dfrac{20}{3}-\dfrac{15}{3}=\dfrac{5}{3}\end{matrix}\right.\)

a, Hàm số \(\left(d_1\right)y=-2x+3\)
Cho \(y=0=>x=\dfrac{3}{2}\) ta được điểm \(\left(\dfrac{3}{2};0\right)\)
Cho \(x=0=>y=3\) ta được điểm \(\left(0;3\right)\)
Vẽ đồ thị hàm số \(\left(d_1\right)\) đi qua hai điểm trên
hàm số \(\left(d_2\right)y=x-1\)
Cho \(y=0=>x=1\) ta được điểm \(\left(1;0\right)\)
Cho \(x=0=>y=-1\) ta được điểm \(\left(0;-1\right)\)
Vẽ đồ thị hàm số \(\left(d_2\right)\) đi qua hai điểm trên
# Bạn có thể tự vẽ nhé !!
b, Tọa độ giao điểm \(\left(d_1\right);\left(d_2\right)\) là nghiệm của pt
\(-2x+3=x-1\\ =>-3x=-4\\ =>x=\dfrac{4}{3}\)
Thay \(x=\dfrac{4}{3}\) vào \(\left(d_2\right)\)
\(\Rightarrow y=\dfrac{4}{3}-1=\dfrac{1}{3}\)
Vậy tọa độ giao điểm là : \(\left(\dfrac{4}{3};\dfrac{1}{3}\right)\)
c, Giả sử \(\left(d_3\right)y=ax+b\)
\(\left(d_3\right)\) đi qua \(A\left(-2;1\right)\) và song song với đường thẳng \(\left(d_1\right)y=-2x+3\)
\(\Rightarrow\left\{{}\begin{matrix}4a+b=1\\a=-2;b\ne3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}4.\left(-2\right)+b=1\\a=-2;b\ne3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b=9\left(t/m\right)\\a=-2\end{matrix}\right.\)
Vậy \(d_3:y=-2x+9\)
#Rinz
`(d_1)` là có dạng như thế nào vậy bạn
(d1) là y= \(\dfrac{1}{2}x-3\)