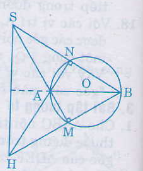
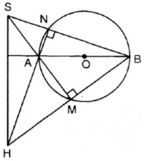
CHo đường tronftaam O đường kính AB và K là 1 điểm nằm nhoài đường tròn. KA và KB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM, AN.
a) Cm: KH vuông góc với AB
b) Cm: góc BMO = góc AKH
c) Cm:Gọi P là tâm đường tròn ngoại tiếp tam gicas KMH. CM: MP là tiếp tuyến của đường tròn
d) Trên tia AN lấy điểm I sao cho AI = BN , qua I kẻ đường thẳng d vuông góc với AN. CM: Đường thẳng d luôn đi qua 1 điểm cố định
MÌNH CHỈ CẦN LÀM CÂU D THÔI CÂU A+B+C MÌNH LÀM ĐƯỢC RỒI
MÌNH CẦN GẤP LẮM NGÀY 28/2 LÀ KIỂM TRA RỒI

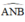 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 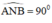 ⇒ AN ⊥ NB
⇒ AN ⊥ NB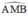 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 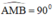 ⇒ AM ⊥ MB
⇒ AM ⊥ MB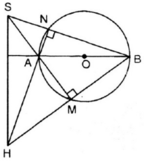
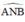 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 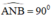 ⇒ AN ⊥ NB
⇒ AN ⊥ NB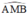 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 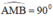 ⇒ AM ⊥ MB
⇒ AM ⊥ MB