Cho 5 đường thẳng cắt nhau tại một điểm , tính số góc được tạo thành ( không kể góc bẹt)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2017
Có 101 đường thẳng nên sẽ có
101.2=202( tia)
Cứ 1 tia tạo với 1 tia được 1 đường thẳng
Lấy 1 tia tạo với 200 tia còn lại đường thẳng ( loại tia đối với tia được chọn)
Làm vậy với 202 tia ta được 200.202 góc ( nhỏ hơn góc bẹt)
Tuy nhiên, số góc đã được tính 2 lần
Vậy thật sự chỉ có \(\frac{200.202}{2}=20200\)( góc)
CM
23 tháng 2 2018
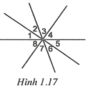
a) Liệt kê các cặp góc đối đỉnh
Xét các cặp góc “đơn”:
Góc 1 đối đỉnh với góc 5; Góc 2 đối đỉnh với góc 6; Góc 3 đối đỉnh với góc 7; Góc 4 đối đỉnh với góc 8. Có tất cả 4 góc “đơn” đối đỉnh.
Xét các cặp góc “ghép đôi” (ghép hai góc đơn kề nhau thành một góc “ghép đôi”):
Góc 12 đối đỉnh với góc 56; Góc 23 đối đỉnh với góc 67; Góc 34 đối đỉnh với góc 78; Góc 45 đối đỉnh với góc 81. Có tất cả 4 cặp góc “ghép đôi” đối đỉnh.
Xét các cặp góc “ghép ba” (ghép ba góc đơn kề nhau thành một góc “ghép ba”):
Góc 123 đối đỉnh với góc 567; Góc 234 đối đỉnh với góc 678; Góc 345 đối đỉnh với góc 781; Góc 456 đối đỉnh với góc 812. Có tất cả 4 cặp góc “ghép ba” đối đỉnh.
Vậy tổng cộng có 4.3 = 12 cặp góc đối đỉnh.
b) Xây dựng công thức tính số cặp góc đối đỉnh.
Có 4 đường thẳng cắt nhau tại một điểm nên có: 4.2 = 8 (tia).
Số góc do 8 tia tạo ra là 8.7 2 = 28 (góc).
Không kể góc bẹt thì số góc còn lại là: 28 − 4 = 24 (góc).
Mỗi góc trong 24 góc này đều có một góc đối đỉnh với nó nên số cặp góc đối đỉnh được tạo thành là 24 : 2 = 12 (cặp).
* Nhận xét: Nếu có n đường thẳng cắt nhau tại một điểm thì số cặp góc đối đỉnh (không kể góc bẹt) được tạo thành là n(n-1).
Thật vậy, số tia do n đường thẳng cắt nhau tại một điểm tạo ra là 2n (tia).
Số góc do 2n tia tạo ra là: 2 n 2 n − 1 2 = n 2 n − 1 .
Không kể n góc bẹt thì số góc còn lại là: n 2 n − 1 − n = 2 n 2 − n − n = 2 n 2 − 2 n = 2 n n − 1 .
Số cặp góc đối đỉnh là: 2 n n − 1 2 = n n − 1 .
CM
29 tháng 9 2018
a) Ta có: n n − 1 = 20 b) Ta có: n n − 1 = 90
n n − 1 = 5.4 ⇒ n = 5 . n n − 1 = 10.9 ⇒ n = 10
Vậy n = 5 . Vậy n = 10 .
CM
16 tháng 1 2019
Ta có: A O C ^ = B O D ^ (hai góc đối đỉnh) mà A O C ^ + B O D ^ = 100 ° nên A O C ^ = B O D ^ = 100 ° : 2 = 50 ° .
Hai góc AOC và BOC kề bù nên B O C ^ = 180 ° − 50 ° = 130 ° .
Do đó A O D ^ = B O C ^ = 130 ° (hai góc đối đỉnh).
18 tháng 2 2021
a, - Tổng số góc không chứ góc bẹt là :
\(\dfrac{6\left(6-1\right)}{2}-3=12\) ( góc )
b, Ta có : \(\dfrac{n\left(n-1\right)}{2}=21\)
\(\Rightarrow n=7\) ( tia )
c, - Gọi số tia lúc ban đầu là n tia .
Theo bài ra ta có phương trình :\(\dfrac{\left(n+1\right)\left(\left(n+1\right)-1\right)}{2}-\dfrac{n\left(n-1\right)}{2}=9\)
\(\Leftrightarrow\dfrac{n\left(n+1\right)}{2}-\dfrac{n\left(n-1\right)}{2}=9\)
\(\Leftrightarrow\dfrac{n}{2}\left(\left(n+1\right)-\left(n-1\right)\right)=\dfrac{n}{2}.\left(n+1-n+1\right)=n=9\)
Vậy ...
M
16 tháng 9 2020
Bài 1 : Bài giải
Ta có : \(\widehat{AOC}=\widehat{BOD}\) ( hai góc đối đỉnh ) mà \(\widehat{AOC}+\widehat{BOD}=100^o\)\(\Rightarrow\text{ }\widehat{AOC}=\widehat{BOD}=\frac{1}{2}\cdot100^o=50^o\)
\(\widehat{AOD}=\widehat{BOC}\) ( hai góc đối đỉnh ) mà \(\widehat{AOD}\) kề bù với \(\widehat{BOD}\) nên \(\widehat{AOD}+\widehat{BOD}=180^o\)
\(\Rightarrow\text{ }\widehat{AOD}+50^o=180^o\text{ }\Rightarrow\text{ }\widehat{AOD}=130^o\)
\(\Rightarrow\text{ }\widehat{AOD}=\widehat{BOC}=130^o\)
M
16 tháng 9 2020
Bài 2 : Bài giải
Ta có:
\(\widehat{MOP}=\widehat{NOQ}\) ( hai góc đối đỉnh )
\(\widehat{NOP}=\widehat{MOQ}\)( hai góc đối đỉnh )
Ta lại có : \(\widehat{MOP}\text{ và }\widehat{NOP}\) là 2 góc kề bù nên \(\widehat{MOP}+\widehat{NOP}=180^o\)
Mà \(\widehat{NOP}=\frac{2}{3}\widehat{MOP}\) nên \(\widehat{MOP}+\frac{2}{3}\widehat{MOP}=180^o\)
\(\Rightarrow\text{ }\frac{5}{3}\widehat{MOP}=180^o\text{ }\Rightarrow\text{ }\widehat{MOP}=108^o\)
\(\Rightarrow\text{ }\widehat{NOP}=\frac{2}{3}\cdot108^o=72^o\)
\(\Rightarrow\text{ }\widehat{MOP}=\widehat{NOQ}=108^o\)
\(\Rightarrow\text{ }\widehat{NOP}=\widehat{MOQ}=72^o\)