Cho tam giác ABC có H là tâm đường tròn ngoại tiếp tam giác; M là trọng tâm; N là trực tâm. Chứng minh 3 điểm H;M;N thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 5 2017
a)
– Tọa độ trọng tâm G của tam giác ABC là:
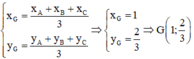
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận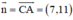 
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận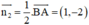 
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
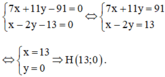
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
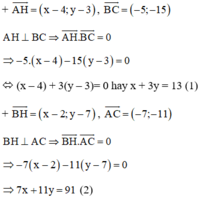
Từ (1) và (2) ta có hệ phương trình
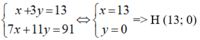
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
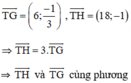
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
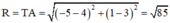
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85
CH
Cô Hoàng Huyền
Admin
VIP
24 tháng 3 2017
a. Ta thấy \(\widehat{HDC}=\widehat{HEC}=90^o\) nên CDHE là tứ giác nội tiếp đường tròn đường kính HC.
b. Ta thấy ngay \(\widehat{IAC}=\widehat{KBC}\) (Cùng phụ với góc ACB) nên \(\widebat{IC}=\widebat{KC}\) (Góc nội tiếp)
suy ra IC = KC ( Liên hệ giữa cung và dây)
Vậy nên tam giác IKC cân tại C.
c. Do \(\widebat{IC}=\widebat{KC}\) nên \(\widehat{KAC}=\widehat{ACI}\) (Góc nội tiếp)
Xét tam giác AHK có AE vừa là đường cao, vừa là phân giác nên AHK là tam giác cân tại A, hay AH = AK.
d. Ta thấy do BOF là đường kính nên \(\widehat{BCF}=90^o\Rightarrow\) AH // FC (Cùng vuông góc với BC).
Tương tự AF // HC vì cùng vuông góc với AB. Vậy thì AFCH là hình bình hành hay AC giao FH tại trung điểm mỗi đường.
P là trung điểm AC nên F cũng là trung điểm FH. Vậy F, H, P thẳng hàng.
30 tháng 4 2020
a . Gọi AH ∩ BC=D,BH ∩ AC=E,CH ∩ AB=F
\(\Rightarrow AD\perp BC,BE\perp AC,CF\perp AB\)
\(\Rightarrow\widehat{ADC}=\widehat{AFC}=90^0\) => ◊AFDC nội tiếp
\(\Rightarrow\widehat{DCF}=\widehat{DAF}\)
VÌ H đối xứng H' qua BC
\(\Rightarrow HH'\perp BC\Rightarrow A,H,,D,H'\)thẳng hàng
\(\Rightarrow\widehat{BAH'}=\widehat{DAF}=\widehat{FDC}=\widehat{HCB}\)
Lại có: H đối xứng với H' qua BC
\(\Rightarrow\widehat{BCH'}=\widehat{HCB}\)
\(\Rightarrow\widehat{BCH'}=\widehat{BAH'}\Rightarrow\)
\(\Rightarrow BC\perp AA'\Rightarrow A,H,D,H',A'\) thẳng hàng
Vì \(H,H'\) đối xứng qua BC , A,A' đối xứng qua BC
\(\Rightarrow\widehat{BHC}=\widehat{BH'C},\widehat{BAC}=\widehat{BA'C}\)
Lại có ◊ ABH'C nội tiếp
\(\Rightarrow\widehat{BAC}+\widehat{BH'C}=180^0\)
\(\Rightarrow\widehat{BA'C}+\widehat{BHC}=180^0\)
=> ◊ BHCA' nội tiếp
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp \(\Delta A'BC\)
Ta có : A , A' đối cứng qua BC
\(\Rightarrow A'B=AB,CA=CA'\Rightarrow\Delta ABC=\Delta A'BC\left(c.c.c\right)\)
=> Bán kính đường tròn ngoại tiếp \(\Delta A'BC\) bằng bán kính đường tròn ngoại tiếp ΔABC
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp ΔABC