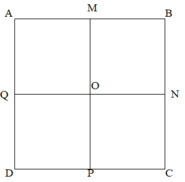
Xác định trung điểm M,N,P,Q của các cạnh AB,BC,CD,DA của hình vuông ABCD.Hai đoạn thẳng MP và NQ cắt nhau tại O tạo thành 4 hình vuông bé. Tính chu vi hình vuông AMOQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 10 2019
Dùng thước đo hình vuông ABCD, có độ dài cạnh là 6cm.
AM = 1 2 AB = 3cm
Chu vi hình vuông AMOQ là: AM x 4 = 3 x 4 = 12 (cm)
Đáp số: 12cm.
CM
16 tháng 1 2018
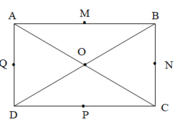
Các đoạn thẳng có độ dài bằng nhau là: AB = CD; AD = BC; AC = BD; AM = MB; BN = NC; CP = PD; DQ = QA; AO = OC = OB = OD.
CM
23 tháng 8 2018
a) Viết tiếp vào chỗ chấm cho thích hợp:
- Trong hình bên có các góc vuông là:
Góc vuông đỉnh C, cạnh CM, CD. Góc vuông đỉnh D, cạnh DC, DN. Góc vuông đỉnh N, cạnh ND, NM. Góc đỉnh M, cạnh MN, MC. Goc vuông đỉnh A, cạnh AB, AE.
- M là trung điểm của đoạn thẳng BC.
- N là trung điểm của đoạn thẳng ED.
b) Xác định trung điểm I của đoạn thẳng MN, trung điểm K của đoạn thẳng CD (bằng cách đánh dấu rồi ghi tên điểm đó trên hình vẽ).
11 tháng 4
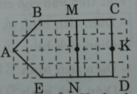
A trong hình bên có........... Góc vuông
B trong hình bên có......... Góc không vuông
C điểm m là trung điểm của đoạn thẳng
D trung điểm của đoạn thẳng.......
E điểm e ở giữa hai điểm....... Và..........,............và.........
21 tháng 11 2017
a) xét tam giác BAD ta có:
M là trung điểm AB (gt)
F là trung điểm BD (gt)
vậy MF là đường trung bình tam giác BAD
=>MF//AD và MF=1/2 AD (1)
xét tam giác ADC ta có:
P là trung điểm CD (gt)
E là trung điểm AC (gt)
vậy PE là đường trung bình tam giác ADC
=>PE//AD và PE=1/2 AD (2)
từ (1) và (2) => PE//MF và PE=MF=1/2 AD
tương tự như vậy với ME và PF ta có được ME//PF và ME=PF=1/2 BC
ta có:
ME=PF=1/2 BC (cmt)
MF=PE=1/2 AD (cmt)
AD=BC (gt)
vậy ME=PF=MF=PE
=>MEPF là hình thoi
b) vẽ tứ giác MQPN. gọi giao điểm QN và MP là K
xét tam giác ABD ta có:
Q là trung điểm AD (gt)
M là trung điểm AB (gt)
vậy MQ là đường trung bình tam giác ABD
=> MQ//BD và MQ=1/2 BD (1)
xét tam giác CBD ta có:
P là trung điểm CD (gt)
N là trung điểm BC (gt)
vậy PN là đường trung bình tam giác CBD
=> PN//BD và PN=1/2 BD (2)
từ (1) và (2)=> PN//MQ và PN=MQ
=>MQPN là hình bình hành
mà QN và MP là hai đường chéo và K là giao điểm
=>K là trung điểm của QN và MP (3)
xét hình thoi MEPF ta có:
MP và EF là hai đường chéo
K là trung điểm MP (cmt)
=> K là trung điểm EF (4)
từ (3) và (4)=> QN,MP,EF đồng quy tại K.
MT
22 tháng 5 2015
Bạn tự vẽ hình
a)*ta có M là trung điểm của AB
N là trung điểm của BC
Suy ra: MN là đường trung bình của tam giác ABC
*ta có N là trung điểm của BC
P là trung điểm của DC
Suy ra : NP là đường trung bình của tam giác BCD
b)ta có Q là trung điểm của AD
P là trung điểm của DC
Suy ra PQ là đường trung bình của tam giác ADC
=>PQ song song với AC;PQ=\(\frac{AC}{2}\)
mà MN song song với AC;MN=\(\frac{AC}{2}\)(MN là đường trung bình của tam giác ABC)
nên: PQ song song MN;PQ=MN
Suy ra MNPQ là hình binh hành(1)
ta lại có : AD=BC(ABCD là hình thang cân)
=>AQ=BN=QD=NC(Q,N lần lượt là trung điểm của AD,BC)
Xét tam giác MNB và tam giác MQA
BN=AQ (chứng minh trên)
MB=MA(M là trung điểm của AB)
góc MAQ=góc MBN
Suy ra tam giác MNB=tam giác MQA(c-g-c)
=>MQ=MN( 2 cạnh tương ứng )(2)
Từ (1) và (2) suy ra :
MNPQ là hình thoi
=> MP vuông góc NQ
