cho tam giác abc,trên ab lấy điểm m làm điểm chính giữa,trên bc lấy n làm điểm chính giữa,trên ac lấy i làm điểm chính giữa .Nối m với n,nối n với i,nối i với m.So sánh diện tích hình tam giác mni với diện tích tam diac abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 3 2023
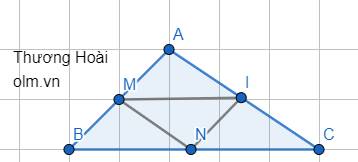
SBMN = \(\dfrac{1}{2}\)SABN ( hai tam giác có chung đường cao và tỉ số hai cạnh đáy tương ứng là \(\dfrac{1}{2}\))
SABN = \(\dfrac{1}{2}\) SABC ( hai tam giác có chung đường cao và tỉ số hai cạnh đáy là \(\dfrac{1}{2}\))
=> SBMN = \(\dfrac{1}{2}\times\dfrac{1}{2}\)SABC = \(\dfrac{1}{4}\) SABC
Chứng minh tương tự ta có :
SAMI = SCNI = \(\dfrac{1}{4}\) SABC
=> SMNI = Mặt khác ta có :
SABC = SBMN + SAMI + SCNI + SMNI
=> SMNI = SABC - SBMN - SAMI
=> SMNI = SABC - \(\dfrac{1}{4}\) SABC - \(\dfrac{1}{4}\) SABC - \(\dfrac{1}{4}\)SABC
=> SMNI = SABC \(\times\)( 1 - \(\dfrac{1}{4}\) - \(\dfrac{1}{4}\) - \(\dfrac{1}{4}\))
=> SMNI = \(\dfrac{1}{4}\)SABC
7 tháng 6 2019
bn có thể tham khảo tại: https://olm.vn/hoi-dap/detail/96626463011.html
DD
Đoàn Đức Hà
Giáo viên
22 tháng 5 2022
a) \(S_{ANB}=\dfrac{1}{2}\times S_{ABC}\) (chung đường cao hạ từ \(B\), \(AN=\dfrac{1}{2}\times AC\))
\(S_{AMC}=\dfrac{1}{2}\times S_{ABC}\) (chung đường cao hạ từ \(C\), \(AM=\dfrac{1}{2}\times AB\))
suy ra \(S_{AMC}=S_{ANB}\).
b) \(S_{MIB}=S_{ANB}-S_{AMIN},S_{NIC}=S_{AMC}-S_{AMIN}\)
mà \(S_{AMC}=S_{ANB}\) suy ra \(S_{MIB}=S_{NIC}\).