Một ô tô đi từ A đến B cách nhau 100km với vận tốc không đổi .Khi từ B về A tăng vận tốc thêm 10km/h so với lúc đi. Vì vậy thời gian đi là 30 phút .Tính vận tốc lúc đi của ô tô.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
Gọi vận tốc lúc đi là x (km/h), x>10
Thời gian đi: \(\dfrac{300}{x}\) giờ
Vận tốc lúc về: \(x-10\)
Thời gian về: \(\dfrac{300}{x-10}\)
Ta có pt: \(\dfrac{300}{x-10}-\dfrac{300}{x}=1\Leftrightarrow300x-300\left(x-10\right)=x\left(x-10\right)\)
\(\Leftrightarrow x^2-10x-3000=0\Rightarrow\left[{}\begin{matrix}x=60\\x=-50\left(loại\right)\end{matrix}\right.\)
24 tháng 2 2021
Gọi x(km/h) là vận tốc lúc đi(Điều kiện: x>0 và \(x\ne10\))
Thời gian ô tô đi từ A đến B là:
\(\dfrac{300}{x}\)(giờ)
Thời gian ô tô đi từ B về A là:
\(\dfrac{300}{x-10}\)(giờ)
Vì thời gian về nhiều hơn thời gian đi là 1 giờ nên ta có phương trình:
\(\dfrac{300}{x-10}-\dfrac{300}{x}=1\)
\(\Leftrightarrow\dfrac{300x}{x\left(x-10\right)}-\dfrac{300\left(x-10\right)}{x\left(x-10\right)}=\dfrac{x\left(x-10\right)}{x\left(x-10\right)}\)
Suy ra: \(300x-300x+3000=x^2-10x\)
\(\Leftrightarrow x^2-10x-3000=0\)
\(\Leftrightarrow x^2-60x+50x-3000=0\)
\(\Leftrightarrow x\left(x-60\right)+50\left(x-60\right)=0\)
\(\Leftrightarrow\left(x-60\right)\left(x+50\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-60=0\\x+50=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=60\left(nhận\right)\\x=-50\left(loại\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đi là 60km/h
14 tháng 1
Gọi vận tốc của ô tô lúc đi từ A đến B là x(km/h)
(Điều kiện: x>0)
Vận tốc của ô tô lúc đi từ B về A là x+10(km/h)
Thời gian ô tô đi từ A đến B là \(\dfrac{400}{x}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{400}{x+10}\left(giờ\right)\)
Theo đề, ta có phương trình:
\(\dfrac{400}{x}-\dfrac{400}{x+10}=2\)
=>\(\dfrac{400x+4000-400x}{x\left(x+10\right)}=2\)
=>2x(x+10)=4000
=>x(x+10)=2000
=>x^2+10x-2000=0
=>(x+20)(x-10)=0
=>\(\left[{}\begin{matrix}x+20=0\\x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-20\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: vận tốc ô tô lúc đi từ A đến B là 10km/h
CM
28 tháng 7 2018
Đáp án D
Gọi vận tốc của ô tô khi đi từ A đến B là x (km/h) (x > 0)
Thời gian ô tô đi từ A đến B là: 156/x (giờ)
Vận tốc của ô tô lúc về là: x + 32 (km) .
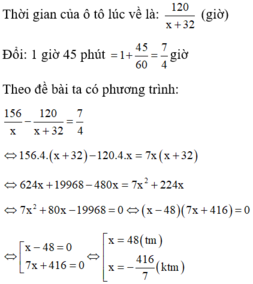
Vậy vận tốc của ô tô lúc đi từ A đến B là 48km/h
5 tháng 5 2017
Lúc về ô tô đó cần đi :
5 + 1 = 6 ( giờ )
Tỉ số thời gian lúc đi và lúc về là :
\(5:6=\frac{5}{6}\)
Vì trên cùng một quãng đường , vận tốc và thời gian là đại lượng có tỉ lệ nghịch mà tỉ lệ thời gian lúc đi và lúc về là \(\frac{5}{6}\)nên tỉ số vận tốc lúc đi và lúc về là \(\frac{6}{5}\)
Coi vận tốc lúc đi là 6 phần bằng nhau , vận tốc lúc về là 5 phần như thế nên hiệu số phần bằng nhau là :
6 - 5 = 1 ( phần )
Giá trị một phần là : 10 : 1 = 10 ( km/giờ )
Vận tốc lúc đi là :
10 x 6 = 60 ( km/giờ )
Đáp số : 60 km/giờ
18 tháng 4 2023
Gọi độ dài AB là x
Thời gian dự kiến là x/40
Thời gian thực tế là 1/4+(x-10)/50
Theo đề, ta có:
\(\dfrac{x}{40}-\dfrac{1}{4}-\dfrac{x-10}{50}=\dfrac{21}{60}=\dfrac{7}{20}\)
=>\(\dfrac{1}{40}x-\dfrac{1}{4}-\dfrac{1}{50}x+\dfrac{1}{5}=\dfrac{7}{20}\)
=>x/200=2/5
=>x=80
TG
8 tháng 5 2021
36p = 0,6h
Gọi a là thời gian ô tô đi từ A đến B
Theo đề ta có:
AB = 30a = (30 + 10). (a - 0,6)
=> 30a = 40. (a - 0,6)
=> 30a - 40a = -24
=> -10a = -24
=> a = 2,4
AB = 30a = 30. 2,4 = 72 (km)
R
8 tháng 5 2021
Đổi : 36 phút = 0,6 giờ
Gọi độ dài của quãng đường AB là s (đơn vị là km, s>0) (1)
=> thời gian khi đi từ A đến B là : \(\dfrac{s}{30}\) (đơn vị là km/h, \(\dfrac{s}{30}\)>0) (2)
=> thời gian khi đi từ B về A là : \(\dfrac{s}{30+10}\)(đơn vị là km/h, \(\dfrac{s}{30+10}\)>0) (3)
Từ (1),(2),(3) theo bài ra ta có :
\(\dfrac{s}{30}-\dfrac{s}{30+10}=0,6\)
<=> s.(\(\dfrac{1}{30}-\dfrac{1}{30+10}\)) = 0,6
<=> s. \(\dfrac{1}{120}\) = 0,6
<=. s = 0,6 : \(\dfrac{1}{120}\) = 72 (km)
Vậy quãng đường AB dài 72 km