một hộp có 4 bi đỏ, 5 bi đen, 6 bi vàng. lấy ngẫu nhiên 3 bi, giả sử mỗi bi đỏ được 1 điểm, mỗi bi đen được -1 điểm, mỗi bi vàng được 0 điểm. tính độ lệch chuẩn của số điểm đó. :D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hộp 1 có 9 viên, hộp 2 có 9 viên, lấy ở mỗi hộp 1 viên.
\(\Rightarrow n(Ω)=(C_{9}^{1})^2=81\)
A: "Hai viên bi chọn được cùng màu".
TH1: cùng màu vàng: \(C_{6}^{1} .C_{5}^{1} =30\)
TH2: cùng màu đỏ: \(C_{3}^{1} .C_{4}^{1}=12\)
\(\Rightarrow n(A)=30+12=42\)
\(\Rightarrow P(A) =\dfrac{n(A)}{n(Ω)}=\dfrac{42}{81}=\dfrac{14}{27}\).

Hộp 1 có 9 viên, hộp 2 có 9 viên, lấy ở mỗi hộp 1 viên.
\(\Rightarrow n(Ω)=(C_{9}^{1})^2=81\)
A: "Hai viên bi chọn được cùng màu".
TH1: cùng màu vàng: \(C_{6}^{1} .C_{5}^{1} =30\)
TH2: cùng màu đỏ: \(C_{3}^{1} .C_{4}^{1}=12\)
\(\Rightarrow n(A)=30+12=42\)
\(\Rightarrow P(A) =\dfrac{n(A)}{n(Ω)}=\dfrac{42}{81}=\dfrac{14}{27}\).

Không gian mẫu là chọn ngẫu nhiên mỗi hộp 2 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh . Ta liệt kê các trường hợp thuận lợi của không gian biến cố A như sau:
● Trường hợp 1. Chọn hộp thứ nhất 2 viên bi đỏ, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Chọn hộp thứ nhất 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 3. Chọn hộp thứ nhất 2 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi đỏ hoặc 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 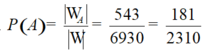
Chọn B.

Đáp án B
Có các cách chọn sau:
+) 1 bi đỏ, 1 bi vàng, 3 bi xanh, suy ra có C 6 1 C 7 1 C 5 3 = 420 cách.
+) 2 bi đỏ, 2 bi vàng, 1 bi xanh, suy ra có C 6 2 C 7 2 C 5 1 = 1575 cách.
Suy ra xác suất bằng 420 + 1575 C 18 5 = 95 408 .


