Cho góc nhọn xAy, trên tia Ax xác định điểm I, trên tia Ay xác định điểm H sao cho AH = AI. Gọi K là trung điểm của đoạn thẳng IH.
*Chứng minh:
a) Tam giác AKI = Tam giác AKH
b) AK là tia phân giác của góc xAy
c) AK vuông góc IH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LP
18 tháng 12 2015
a )
Xét tam giác ABM và tam giác ACM có:
BM = MC ( vì M là trung điểm của BC )
AM là cạnh chung
AB = AC ( gt )
=> tam giác ABM = tam giác ACM ( c.c.c )
b) Xét tam giác AEH và tam giác CEM có:
EH = EM (gt)
góc AEM = góc MEC (2 góc đối đỉnh )
AE = EC ( vì E là trung điểm của AC )
=> tam giác AEK = tam giác CEM (c.g.c)
c) Câu này giải thích nhiều mà tớ không có thời gian nên không ghi ra được. Tích hay không tùy cậu
28 tháng 1 2023
`a,` Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (g``t)`
AI chung
`IB = IC (g``t)`
`=>` Tam giác `AIB =` Tam giác `AIC (c-c-c)`
`b,` Vì Tam giác `AIB =` Tam giác `AIC (a)`
`=>` \(\widehat{AIB}=\widehat{AIC}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù
`=>` \(\widehat{AIB}+\widehat{AIC}=180^0\)
`=>` \(\widehat{AIB}=\widehat{AIC}=\) \(\dfrac{180}{2}=90^0\)
`=>` \(AI\perp BC\)
Tam giác `ABC` có `IB = IC`, \(AI\perp BC\)
`=> AI` là đường trung trực của `BC (đpcm)`
7 tháng 9 2021
A: Ta có tam giác ABC cân tại A.
=>AB=AC(2cạnh tương ứng)
Xét tam giác ABH và tam giác ACH có:
AB:Cạnh chung
GÓC BAH= GÓC CAH(Theo bài ra)
AB=AC(Cmt)
=>Tam giác ABH=Tam giác ACH(c.g.c)
Phần B thì nghỉ dịch nhiều quá nên mk ko biết nó đối theo hướng nào nên ko làm đc. Sorry bn😪
CHÚC BN HOK TỐT.😍
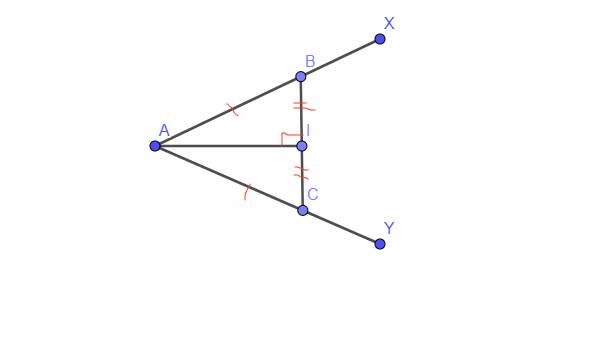
Bạn vẽ hình giùm mình nhé!
a) Xét tam giác AKI và tam giác AKH có:
IK = KH (k trđ IH)
AI = AH (gt)
AK cạnh chung
Nên tam giác AKI bằng tam giác AKH (ccc)
b) Từ c./m a có: tam giác AKI = tam giác AKH
=> góc IAK = góc HAK
Kết hợp AK nằm giữa AI và AH
=> AK p/g IAH hay AK p/g xAy
c) Có: tam giác AKI = tam giác AKH
=> góc AKI = GÓC AKH
mà AKI + AKH = 180 dộ (kề bù)
=> AKI=AKH =180 độ : 2 = 90 độ
=> AK vuông IH