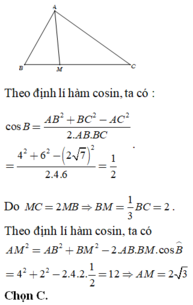tam giác ABC có AB=4,BC=6,AC=\(2\sqrt{7}\).Điểm M thuộc đoạn BC sao cho MC=2MB.Tính độ dài cạnh AM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VY
Vi Yến
18 tháng 4 2021
Đúng(2)
Những câu hỏi liên quan
CM
14 tháng 8 2017
Chọn C.
Theo định lí hàm cosin, ta có : 
Do MC = 2MB nên BM = 1/3.BC = 2.
Theo định lí hàm cosin, ta có: AM2 = AB2 + BM2 - 2AB.BM.cos B = 42 + 22 -2.4.2.1/2 = 12
Do đó: 
.
30 tháng 7 2023
Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AN/4=3/5
=>AN=2,4cm
6 tháng 5 2016
Câu a)
Ta có MN//BC ( giả thiết)
=>AM/AB=MN/BC ( định lí ta lét )
=>MN=AM.BC/AB=3.8/4=6(cm)
*BD=?
Ta có AD là phân giác ( giả thiết )
=>BD/DC=AB/AC (tính chất đường phân giác )
=>BD/(BD+DC)=4/4+6=2/5
=>BD/BC=2/5=2,4 (cm)
*MI=?
Ta có MN//BC (gthiet)
=>MI//BD
=>AM/AB=MI/BD (định lí ta let )
=>MI=MA.BD/AB=3.2,4/4=1,8 (cm)
bạn còn bài nào ko mk giai dùm cho nếu mk biết
K
12 tháng 3 2023
a) Do MN//BC nên theo hệ quả của ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)
\(\Rightarrow\) \(\dfrac{2}{4}\) = \(\dfrac{MN}{6}\)\(\Rightarrow\) MN = \(\dfrac{2\times6}{4}\)\(\Rightarrow\) MN = 3 cm
b) Do MN//BC nên theo ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AC}\)
\(\Rightarrow\)\(\dfrac{12}{15}\)=\(\dfrac{AN}{18}\)\(\Rightarrow\) AN = \(\dfrac{12\times18}{15}\) = 14,4 cm
P
22 tháng 4 2017
nhớ tk cho ming nha
1, Xét tam giác ABC có :
\(BC^2=AC^2+AB^2\)
\(\Leftrightarrow BC^2=4^2+3^2\)
\(\Leftrightarrow BC^2=25\)
\(\Leftrightarrow BC=5\left(cm\right)\)
2,Ta có :\(\widehat{BMA}+\widehat{MBA}=90^O\)
\(\widehat{BMH}+\widehat{MBH}=90^O\)
MÀ \(\widehat{ABM}=\widehat{HBM}\)
Nên \(\widehat{BMA}=\widehat{BMH}\)
Xét tam giác ABM và tam giác HBM có :
\(\widehat{ABM}=\widehat{HBM}\left(gt\right)\)
\(BMchung\)
\(\widehat{BMA}=\widehat{BMH}\)
\(\Rightarrow\Delta BAM=\Delta BHM\left(c.g.c\right)\)
3,Vì \(\Delta BAM=\Delta BHM\Rightarrow AM=MH\left(1\right)\)
Xét \(\Delta HMC\)có :
\(\widehat{MHC}=90^0\)
Suy ra :MC>MH(2)
Từ (1) và(2):AM<MC
4,Ta có :\(\widehat{AMH}+\widehat{HMC}=180^0\left(1\right)\)
Xét tam giác NMA và tam giác CMH có:
\(HC=NA\)
\(\widehat{NAM}=\widehat{CHM}\)
\(MA=MH\left(\Delta BAM=\Delta BHM\right)\)
\(\Rightarrow\Delta NMA=\Delta CMH\left(c.g.c\right)\)
\(\Rightarrow\widehat{NMA}=\widehat{CMH}\)(2)
Từ (1) và(2) : => N,M,H thẳng hàng