Tìm x,y: (3x-4y+34)^2 + l2x+3yl <= 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QA
1
6 tháng 9 2015
|2x - 1| + |1 - y| = 0
=> 2x - 1 = 0
=> 2x = 1
=> x = 1/2
=> 1-y = 0
=> y = 1 - 0 = 0
Vậy x = 1/2 tại y = 0
|x - 3y| + (y+1)2 = 0
=> \(\left(y+1\right)^2=0\rightarrow y+1=0;y=-1\)
Thay vào ta có: |x - 3.(-1) | = 0
=> x - (-3) = 0
=> x =-3
Vây x = -3 tại y = -1
NM
3
26 tháng 12 2017
Ta có: |2x+3y|\(\ge0\)
|4y+5z|\(\ge0\)
|xy+yz+xz+110|\(\ge0\)
\(\Rightarrow\) l2x+3yl+l4y+5zl+lxy+yz+xz+110l\(\ge0\)
hay P \(\ge0\)
\(\Rightarrow\)GTNN của P=0
Dấu "="xảy ra khi:
\(\hept{\begin{cases}\left|2x+3y\right|=0\\\left|4y+5z\right|=0\\\left|xy+yz+xz+110\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}2x+3y=0\\4y+5z=0\\xy+yz+xz+110=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\\\\xy+yz+xz=-110\end{cases}}\)
S
21 tháng 4 2023
\(3x=4y\)
\(\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\)
\(\Rightarrow\dfrac{2x}{8}=\dfrac{3y}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{2x}{8}=\dfrac{3y}{24}=\dfrac{2x+3y}{8+9}=\dfrac{34}{17}=2\)
\(\Rightarrow x=2\cdot4=8\)
\(y=2\cdot3=6\)
H
3 tháng 12 2023
a)
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{3x-2y}{3.5-2.2}=\dfrac{-55}{11}=-5\)
=> \(\left\{{}\begin{matrix}x=-5.5=-25\\y=-5.2=-10\end{matrix}\right.\)
b)
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{2x+5y}{2.3+5.2}=\dfrac{48}{16}=3\)
=> \(\left\{{}\begin{matrix}x=3.3=9\\y=3.2=6\end{matrix}\right.\)
c)
Có: \(\dfrac{x}{y}=-\dfrac{5}{2}\Leftrightarrow-\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x+y}{-5+2}=\dfrac{30}{-3}=-10\)
=> \(\left\{{}\begin{matrix}x=-10.-5=50\\y=-10.2=-20\end{matrix}\right.\)
d)
Có: \(\dfrac{x}{y}=\dfrac{4}{3}\Leftrightarrow\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{2x+3y}{2.4+3.3}=\dfrac{34}{17}=2\)
=> \(\left\{{}\begin{matrix}x=2.4=8\\y=2.3=6\end{matrix}\right.\)
CM
17 tháng 9 2018
Nhân cả tử và mẫu của tỉ số thứ nhất, thứ hai và thứ ba của (1) lần lượt với -3; -4 ; 5 ta được
TT
0
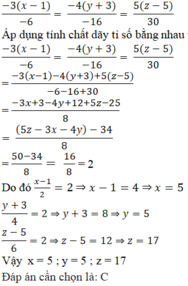
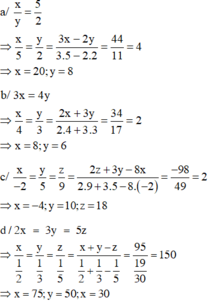
\(\hept{\begin{cases}3x-4y+34=0\\I2x+3yI=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}\left(2x+3y\right)-7y+34=0\\I2x+3yI=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}y=\frac{34}{7}\\x=-\frac{3y}{2}=-\frac{3.17}{7}\end{cases}}\)