Giúp mình giải bài 5 phần d với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
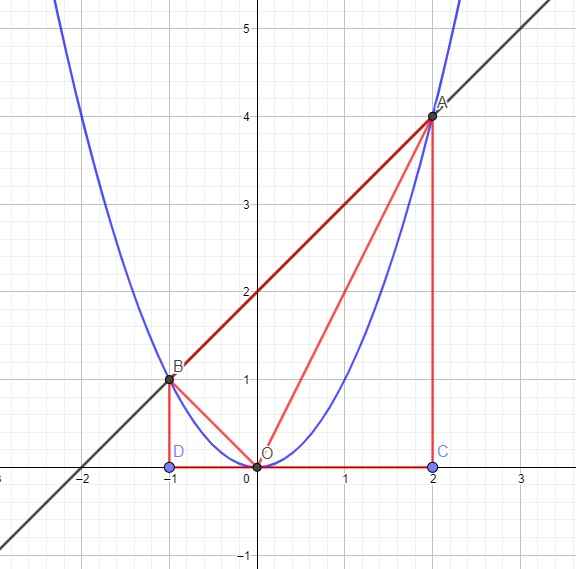
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)
NH
1
NH
2
H
26 tháng 12 2022
Giải :
\(\dfrac{x+11}{89}+\dfrac{x+13}{87}-\dfrac{x+15}{85}-\dfrac{x+17}{83}=0\\ =>\left(\dfrac{x+11}{89}+1\right)+\left(\dfrac{x+13}{87}+1\right)-\left(\dfrac{x+15}{85}+1\right)-\left(\dfrac{x+17}{83}+1\right)=0\\ =>\left(\dfrac{x+11+89}{89}\right)+\dfrac{x+13+87}{87}-\dfrac{x+15+85}{85}-\dfrac{x+17+83}{83}=0\\ =>\dfrac{x+100}{89}+\dfrac{x+100}{87}-\dfrac{x+100}{85}-\dfrac{x+100}{83}=0\\ =>\left(x+100\right)\left(\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}\right)=0\\ =>\left[{}\begin{matrix}x+100=0\\\dfrac{1}{89}+\dfrac{1}{87}-\dfrac{1}{85}-\dfrac{1}{83}=0\left(voli\right)\end{matrix}\right.=>x=-100\)
NH
1
NH
2
H
26 tháng 12 2022
\(2x=3y\\ =>\dfrac{x}{3}=\dfrac{y}{2}\\ 4y=5z\\ =>\dfrac{y}{5}=\dfrac{z}{4}\\ \dfrac{x}{3}=\dfrac{y}{2}\\ =>\dfrac{x}{3.5}=\dfrac{y}{2.5}\\ =>\dfrac{x}{15}=\dfrac{y}{10}\\ \dfrac{y}{5}=\dfrac{z}{4}\\ =>\dfrac{y}{5.2}=\dfrac{z}{4.2}\\ =>\dfrac{y}{10}=\dfrac{z}{8}\\ =>\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{8}=\dfrac{x+y+z}{15+10+8}=\dfrac{11}{33}=\dfrac{1}{3}\\ =>\left\{{}\begin{matrix}x=\dfrac{1}{3}.15=5\\y=\dfrac{1}{3}.10=\dfrac{10}{3}\\z=\dfrac{1}{3}.8=\dfrac{8}{3}\end{matrix}\right.\)
NH
2
H
26 tháng 12 2022
Giải
\(\dfrac{x}{3}=\dfrac{y}{4}\\ \Leftrightarrow\dfrac{x}{3.3}=\dfrac{y}{4.3}\\\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{12}\\ \dfrac{y}{3}=\dfrac{z}{5}\\ \Leftrightarrow \dfrac{y}{3.4}=\dfrac{z}{5.4}\\ \Leftrightarrow\dfrac{y}{12}=\dfrac{z}{20}\\ =>\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}=\dfrac{2x+3x+z}{2.9+3.12+20}=\dfrac{6}{74}=\dfrac{3}{37}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{37}\times9=\dfrac{27}{37}\\y=\dfrac{3}{37}\times12=\dfrac{36}{37}\\z=\dfrac{3}{37}\times20=\dfrac{60}{37}\end{matrix}\right.\)
NH
2
NH
2
H
26 tháng 12 2022
\(a,\dfrac{3^{10}.11+9^5.5}{27^3.2^4}.x=-9\\ =>\dfrac{3^{10}.11+\left(3^2\right)^5.5}{\left(3^3\right)^3.2^4}.x=-9\\ =>\dfrac{3^{10}.\left(11+5\right)}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.16}{3^9.2^4}.x=-9\\ =>\dfrac{3^{10}.2^4}{3^9.2^4}.x=-9\\ =>3^1.x=-9\\ =>x=-9:3\\ =>x=-3\)
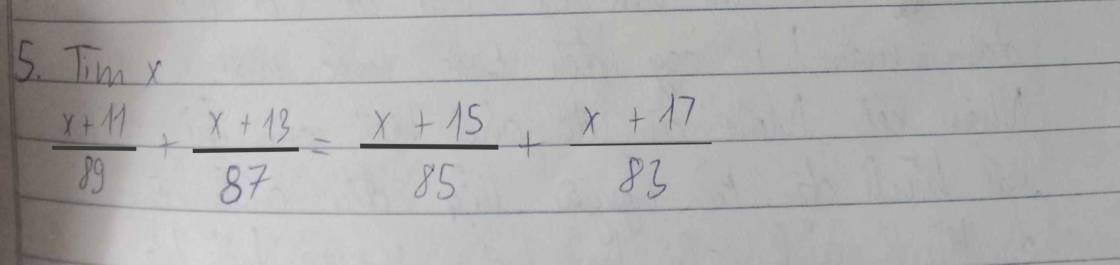
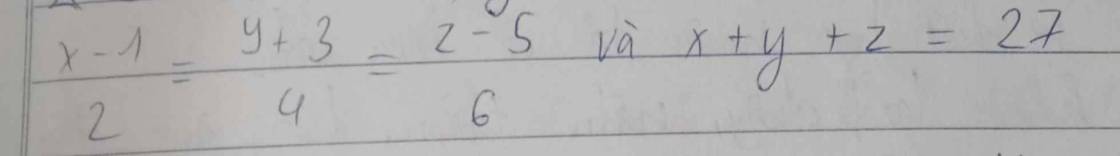
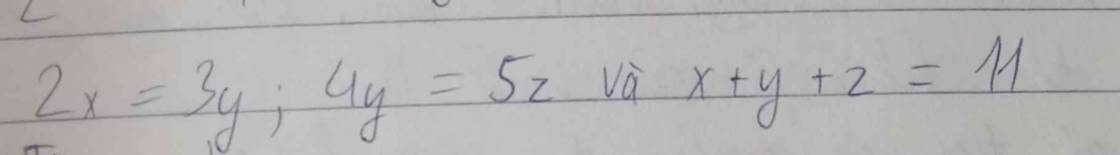
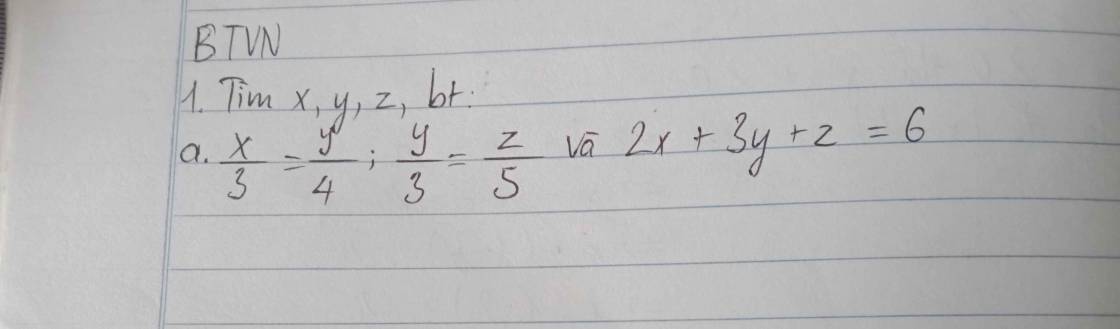
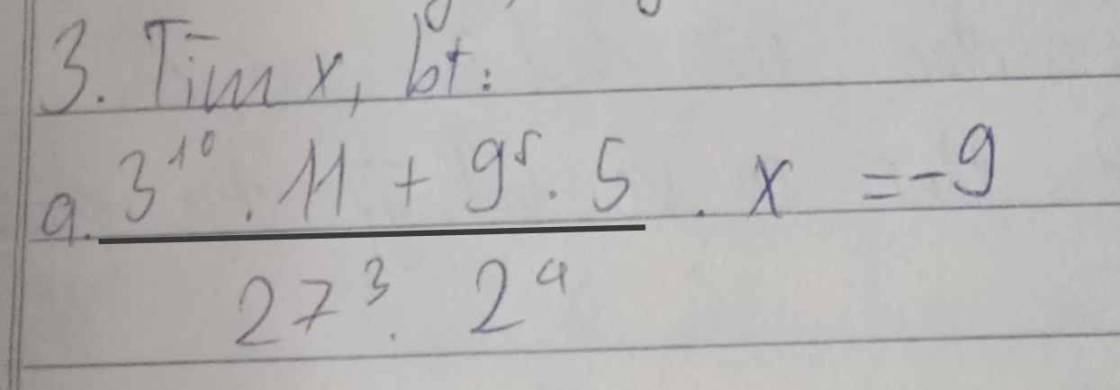
a, bạn tự sắp xếp nhé
b, Ta có : \(P\left(x\right)+Q\left(x\right)\)hay
\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x-2x^5+3x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=6x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
Ta có \(P\left(x\right)-Q\left(x\right)\)hay
\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x+2x^5-3x^4+2x^3-4x^2+\dfrac{1}{4}\)
\(=4x^5-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)
Giá trị x=0 là nghiệm của P(x) vì ko có hệ số tự do => GT là 0
Cái còn lại 1/4 là hệ số tự do => x=0 ko phải là nghiệm của Q(x)