Cho x và y tỉ lệ nghịch biết x1=5 , x2=2 và y1+y2=21 . Tính y1 và y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2022
Vì x,y tỉ lệ nghịch nên \(x_1y_1=x_2y_2\)
\(\Rightarrow\dfrac{y_1}{x_2}=\dfrac{y_2}{x_1}=\dfrac{y_1}{2}=\dfrac{y_2}{5}=\dfrac{y_2+y_1}{2+5}=\dfrac{21}{7}=3\\ \Rightarrow\left\{{}\begin{matrix}y_1=2\cdot3=6\\y_2=3\cdot5=15\end{matrix}\right.\)
4 tháng 3 2020
a) Ta có : \(\frac{x_1}{x_2}=\frac{y_2}{y_1}\Rightarrow\frac{y_1}{x_2}=\frac{y_2}{x_1}=\frac{y_1+y_2}{x_2+x_1}\left(1\right)\)
Vì \(x_1=5,x_2=2\)và \(y_1+y_2=21\)nên từ \(\left(1\right)\)ta có :
\(\frac{y_1}{2}=\frac{y_2}{5}=\frac{y_1+y_2}{2+5}=\frac{21}{7}=3\left(2\right)\)
Từ (2) => \(\orbr{\begin{cases}\frac{y_1}{2}=3\\\frac{y_2}{5}=3\end{cases}}\Rightarrow\orbr{\begin{cases}y_1=6\\y_2=15\end{cases}}\)
b) Ta có : \(\frac{x_1}{x_2}=\frac{y_2}{y_1}=\frac{2x_1}{2x_2}=\frac{3y_2}{3y_1}=\frac{2x_1-3y_2}{2x_2-3y_1}\left(1\right)\)
Vì \(x_2=3,y_1=7\)và \(2x_1-3y_2=30\)nên từ \(\left(1\right)\)ta có :
\(\frac{x_1}{3}=\frac{y_2}{7}=\frac{2x_1-3y_2}{2\cdot3-3\cdot7}=\frac{30}{-15}=-2\left(2\right)\)
Từ \(\left(2\right)\)suy ra : \(\orbr{\begin{cases}\frac{x_1}{3}=-2\\\frac{y_2}{7}=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x_1=-6\\y_2=-14\end{cases}}\)
Câu b x2 = 3(tính rồi nhé,sửa câu đó lại nhé),phải tính x1 và y2 mới đúng.
CM
20 tháng 1 2018
Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 1 = 2 , x 2 = 5 và y 1 + y 2 = 21 .
Do đó 2 y 1 = 5 y 2 ⇒ y 1 5 = y 2 2
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
1 tháng 12 2020
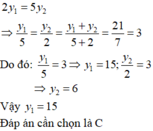
x và y đại lượng tỉ lệ nghịch
x1x2=y2y1hay x1 và x2 ta có:
23=y2y1⇒y13=y22
Mà y12+y22=52
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
y13=y22=y12+y2232+22=5213=4
⇒y13=4⇒y1=12
⇒y22=4⇒y2=8
ta có x=a/y
nên x1+x2=a/y1+y2
hay7=a/21
a=7*21=147