cho ba số x,y,z thỏa mãn x+y+z=2 cmr: xy+2yz+2zx >=3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
27 tháng 9 2023
Lời giải:
Từ $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$
$\Rightarrow xy+yz+xz=0$
Khi đó:
$x^2+2yz=x^2+yz-xz-xy=(x^2-xy)-(xz-yz)=x(x-y)-z(x-y)=(x-z)(x-y)$
Tương tự với $y^2+2zx, z^2+2xy$ thì:
$P=\frac{yz}{(x-z)(x-y)}+\frac{xz}{(y-z)(y-x)}+\frac{xy}{(z-x)(z-y)}$
$=\frac{-yz(y-z)-xz(z-x)-xy(x-y)}{(x-y)(y-z)(z-x)}=\frac{-[yz(y-z)+xz(z-x)+xy(x-y)]}{-[xy(x-y)+yz(y-z)+xz(z-x)]}=1$
8 tháng 12 2021
Ap dụng bất đẳng thức BDT Caucchy Schwarz ta có :
\(\frac{x^2}{x^2+2yz}+\frac{y^2}{y^2+2zx}+\frac{z^2}{z^2+2xy}\)
\(=\frac{\left(x+y+z\right)^2}{x^2+2yz+y^2+2zx+z^2+2xy}\)
\(=\frac{\left(x+y+z\right)^2}{\left(x+y+z\right)^2}=1\)
6 tháng 8 2020
Ta có: \(\frac{x^2}{1+2yz}+\frac{y^2}{1+2zx}+\frac{z^2}{1+2xy}\)
\(\ge\frac{\left(x+y+z\right)^2}{3+2\left(xy+yz+zx\right)}\ge\frac{\left(x+y+z\right)^2}{3+2\left(x^2+y^2+z^2\right)}\)
\(=\frac{\left(x+y+z\right)^2}{3+2}=\frac{\left(x+y+z\right)^2}{5}\)
Mà \(\left(x+y+z\right)^2\le3\left(x^2+y^2+z^2\right)=3\)
Nên thay vào ngược dấu
=> ch bt lm
T
6 tháng 8 2020
Nói chung khá đơn giản. Em chứng minh bất đẳng thức sau đây là được.
\(\frac{x^2}{1+2yz}=\frac{x^2}{x^2+\left(y^2+z^2+2yz\right)}=\frac{x^2}{x^2+\left(y+z\right)^2}\ge\frac{1}{25}\cdot\frac{17x^2-y^2-z^2}{x^2+y^2+z^2}\)
Có thể chứng minnh nó bằng cách: \(f\left(x,y,z\right)=\frac{x^2}{x^2+\left(y+z\right)^2}-\frac{1}{25}\cdot\frac{17x^2-y^2-z^2}{x^2+y^2+z^2}\)
Ta chứng minhL \(f\left(x,y,z\right)\ge f\left(x,\frac{y+z}{2},\frac{y+z}{2}\right)\ge0\) (quy đồng phát là ra nhân tử (y-z)^2 nên hiển nhiên:v)
Tương tự cộng lại. Xong.
Cách Cauchy-SChwarz:
Chứng minh theo trình tự: \(\Sigma\frac{x^2}{x^2+\left(y+z\right)^2}\ge\frac{\left(x^2+y^2+z^2\right)^2}{\Sigma x^2\left[x^2+\left(y+z\right)^2\right]}\ge\frac{3}{5}\)
C
17 tháng 2 2020
\(RHS\ge\frac{\left(x+y+z\right)^2}{\sqrt{5x^2+2xy+y^2}+\sqrt{5y^2+2yz+z^2}+\sqrt{5z^2+2zx+x^2}}\)
Thử chứng minh \(\sqrt{5x^2+2xy+y^2}\le\frac{3\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y\) cái này xem sao
khi đó:
\(RHS\ge\frac{9}{\frac{3\sqrt{2}}{2}\left(x+y+z\right)+\frac{\sqrt{2}}{2}\left(x+y+z\right)}=\frac{3}{2\sqrt{2}}\)
Dấu "=" xảy ra tại x=y=z=1
20 tháng 2 2020
Cần chứng minh BĐT sau : \(\frac{x^2}{\sqrt{5x^2+2xy+y^2}}\ge\frac{5x-y}{8\sqrt{2}}\)
\(\Leftrightarrow8\sqrt{2}x^2\ge\left(5x-y\right)\sqrt{5x^2+2xy+y^2}\) ( 1 )
Xét 5x - y \(\le\)0 \(\Rightarrow\)VT \(\ge\)0 ; VP \(\le\)0 \(\Rightarrow\)BĐT đã được chứng minh
Xét 5x - y \(\ge\)0 . Bình phương 2 vế của ( 1 ), ta được :
\(128x^4\ge\left(25x^2-10xy+y^2\right)\left(5x^2+2xy+y^2\right)\)
\(\Leftrightarrow128x^4\ge125x^4+10x^2y^2-8xy^3+y^4\)
\(\Leftrightarrow3x^4-10x^2y^2+8xy^3-y^4\ge0\)
\(\Leftrightarrow\left(3x^4-3xy^3\right)+\left(10xy^3-10x^2y^2\right)+\left(xy^3-y^4\right)\ge0\)
\(\Leftrightarrow3x\left(x-y\right)\left(x^2+xy+y^2\right)+10xy^2\left(y-x\right)+y^3\left(x-y\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)\left(3x^3+3x^2y+3xy^2-10xy^2+y^3\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)\left[\left(3x^3-3xy^2\right)+\left(3x^2y-3xy^2\right)-\left(xy^2-y^3\right)\right]\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\left(3x^2+6xy-y^2\right)\ge0\)( luôn đúng )
( Vì \(5x-y\ge0\Rightarrow x\ge\frac{y}{5}\)\(\Rightarrow3x^2+6xy-y^2\ge3.\left(\frac{y}{5}\right)^2+6.\frac{y}{5}.y-y^2=\frac{8}{25}y^2\ge0\))
Tương tự : \(\frac{y^2}{\sqrt{5y^2+2yz+z^2}}\ge\frac{5y-z}{8\sqrt{2}}\); \(\frac{z^2}{\sqrt{5z^2+2xz+x^2}}\ge\frac{5z-x}{8\sqrt{2}}\)
Cộng từng vế 3 BĐT lại với nhau, ta được :
\(\frac{x^2}{\sqrt{5x^2+2xy+y^2}}+\frac{y^2}{\sqrt{5y^2+2yz+z^2}}+\frac{z^2}{\sqrt{5z^2+2xz+x^2}}\)
\(\ge\frac{5x-z+5y-z+5z-x}{8\sqrt{2}}=\frac{4\left(x+y+z\right)}{8\sqrt{2}}=\frac{3}{2\sqrt{2}}\)
Dấu "=' xảy ra khi x = y = z = 1
Vậy BĐT đã được chứng minh
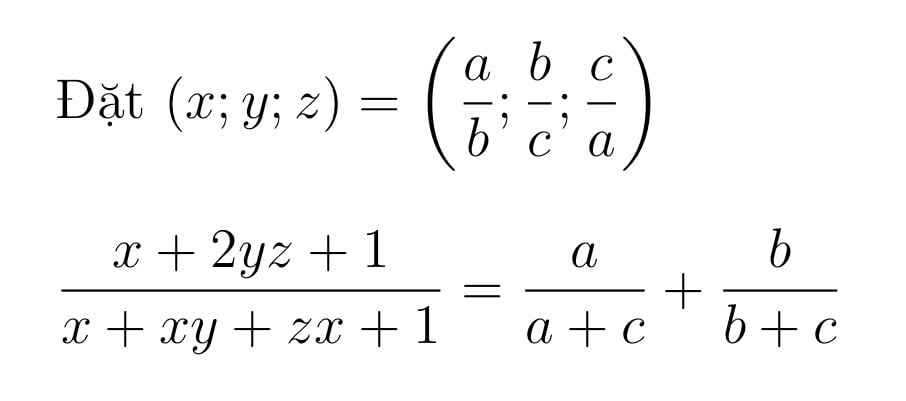
-Đề sai.
Giả sử \(x=\dfrac{1}{3};y=\dfrac{2}{3};z=1\Rightarrow x+y+z=2\)
\(\dfrac{1}{3}.\dfrac{2}{3}+2.\dfrac{2}{3}.1+2.1.\dfrac{1}{3}=\dfrac{20}{9}< 3\)
cmr: xy+2yz+3zx<=3