1 khối khí có áp suất 760mmhg thể tích 100cm³ ở nhiệt độ 27°c nếu áp suất giảm còn 750mmhg và nhiệt độ tăng 127°c thì thể tích là bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 2 2018
Chọn đáp án C
Áp dụng phương trình trạng thái cho khí lí tưởng ta có:
p 1 V 1 T 1 = p 2 V 2 T 2 → T h a y s o 750.40 27 + 273 = 760. V 2 0 + 273 ⇒ V 2 = 35 , 9 c m 3
21 tháng 5 2022
\(a,\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow T_2=\dfrac{T_1p_2}{p_1}=\dfrac{303.4.10^5}{2.10^5}=606^oK\\ b,T_2=\dfrac{303.10^5}{2.10^5}=151,5^oK\)
HT
10 tháng 3 2021
trạng thái 1: V1=2 m3 , p1=2 atm
trạng thái 2: V2= ? , p2=1 atm
áp dụng định luật bôi-lơ-ma-ri-ốt : p1V1=p2V2
\(\Rightarrow\) V2= p1V1/p2 = 4 m3
1 tháng 3 2022
\(T=27^oC=27+273=300K\)
a)Nếu \(p'=\dfrac{1}{2}p=1atm\), áp dụng quá trình đẳng nhiệt:
\(p_1\cdot V_1=p_2\cdot V_2\Rightarrow2\cdot3=1\cdot V_2\)
\(\Rightarrow V_2=6l\)
b)Nếu \(V'=2+V=2+3=5l\), áp dụng quá trình đẳng nhiệt:
\(p_1\cdot V_1=p_2\cdot V_2\Rightarrow2\cdot3=p_2\cdot5\)
\(\Rightarrow p_2=1,2atm\)
VT
19 tháng 5 2018
Đáp án: A
Ta có:
- Trạng thái 1: p 1 ; V 1 ; T 1
- Trạng thái 2: p 2 = p 1 + 0,2 p 1 = 1,2 p 1 V 2 = V 1 − 0,1 V 1 = 0,9 V 1 T 2 = T 1 + 16
Áp dụng phương trình trạng thái của khí lý tưởng, ta có:
p 1 V 1 T 1 = p 2 V 2 T 2 ↔ p 1 V 1 T 1 = 1,2 p 1 .0,9 V 1 T 1 + 16 → T 1 = 200 K
VT
30 tháng 11 2018
Đáp án A
Gọi P0 và V0 là áp suất và thể tích ban đầu của khối khí. Gọi P1 và V1 là áp suất và thể tích của khối khí áp suất của nó tăng lên 3.105Pa
P1 =P0 + 2.105Pa; V1 = V0 - 3 lít
Vì nhiệt độ là không đổi, do đó áp dụng định luật Bôi-lơ-ma-ri-ốt, ta có:P0V0 = (P0 + 2.105)(V0 - 3)
⟹ P0V0 = P0V0 + 2.105V0 - 3V0 - 6.105
⟹ 3P0 = 2.105(V0 - 3)
Gọi P2 và V2 là áp suất và thể tích của khối khí khi áp suất của nó tăng lên 5.105Pa
⟹P1=P0+5.105Pa; V1=V0-5
Tương tự như trên, ta suy ra được:
5P0 = 5.105(V0 - 5)
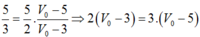(2)
Từ (1) và (2) ta có:
⟹V0 = 15-6 = 9 lít
Thay V0=9 lít và phương trình (1), ta tìm được P0 = 4.105Pa
28 tháng 4 2022
600cm3 = 0,6l
100cm3 = 0,1l
Ta có
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\\ \Rightarrow T_2=\dfrac{p_2V_2.T_1}{p_1V_1}=\dfrac{8.0,1.323}{1.0,6}=430,6^oK\\ \Rightarrow t=157,6^o\)
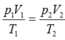
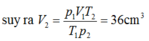
\(\left\{{}\begin{matrix}760mmHg=1atm\\750mmHg\approx0,9atm\end{matrix}\right.\)
Ta có
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\\ \Leftrightarrow\dfrac{1.0,1}{300}=\dfrac{0,9V_2}{400}\Rightarrow V_2\approx0,148=148cm^3\)