mấy anh thánh giúp em câu này với ạ
a) Tìm các số nguyên a sao cho biểu thức P= \(\dfrac{8a+15}{4a+1}\)nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{3\left(n-1\right)+5}{n-1}=3+\dfrac{5}{n-1}\in Z\\ \Leftrightarrow n-1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)

cau 1:8/45:8/9-2/5.x=8/45*9/8-2/5.x=8.9/45.8-2/5.x=1/5-2/5.x=2/-3. =>2/5.x=1/5-2/-3=3/15+2/3=3/15+10/15=13/15. =>x=13/15:2/5=13/15.5/2=13.5/15.2=13/6. Vậy x = 13/6. k nha co j ket ban
8/45 : 8/9 - 2/5 . X = 2/-3
8/45 . 9/8 - 2/5 . X = -2/3
1/5 - 2/5 . X = -2/3
-1/5 . X = -2/3
X = -2/3 : -1/5
X = -2/3 x 5/-1 = 10/3
=> x = 10/3
tk ủng hộ nhé !
nếu có sai nhờ anh/ chị / bạn sửa giùm em ạ !!!!!

a: ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\ne4\end{matrix}\right.\)
\(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-2}+\dfrac{\sqrt{a}}{\sqrt{a}-2}\right)\cdot\dfrac{a-4}{\sqrt{4a}}\)
\(=\dfrac{2\sqrt{a}}{\sqrt{a}-2}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{2a}\)
\(=\sqrt{a}+2\)
b: A-2<0
=>\(\sqrt{a}+2-2< 0\)
=>\(\sqrt{a}< 0\)
=>\(a\in\varnothing\)
c: Bạn ghi đầy đủ đề đi bạn

Ta có:\(6A=\dfrac{6\sqrt{x}}{6\sqrt{x}+1}=\dfrac{6\sqrt{x}+1-1}{6\sqrt{x}+1}=1-\dfrac{1}{6\sqrt{x}+1}\)
Để \(A\in Z\) thì \(\dfrac{1}{6\sqrt{x}+1}=1\Leftrightarrow6\sqrt{x}+1=1\Leftrightarrow6\sqrt{x}=0\Leftrightarrow x=0\)
Với x=0 => A=0

a:
ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\ne4\end{matrix}\right.\)
\(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-2}+\dfrac{\sqrt{a}}{\sqrt{a}+2}\right)\cdot\dfrac{a-4}{\sqrt{4a}}\)
\(=\dfrac{\sqrt{a}\left(\sqrt{a}+2\right)+\sqrt{a}\left(\sqrt{a}-2\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\cdot\dfrac{a-4}{2\sqrt{a}}\)
\(=\dfrac{a+2\sqrt{a}+a-2\sqrt{a}}{a-4}\cdot\dfrac{a-4}{2\sqrt{a}}=\dfrac{2a}{2\sqrt{a}}=\sqrt{a}\)
b: A-2<0
=>\(\sqrt{a}-2< 0\)
=>\(\sqrt{a}< 2\)
=>0<=a<4
kết hợp ĐKXĐ, ta được: 0<a<4
c: Để \(\dfrac{4}{A+1}=\dfrac{4}{\sqrt{a}+1}\) là số nguyên thì
\(\sqrt{a}+1\inƯ\left(4\right)\)
=>\(\sqrt{a}+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{a}\in\left\{0;-2;1;-3;3;-5\right\}\)
=>\(\sqrt{a}\in\left\{0;1;3\right\}\)
=>\(a\in\left\{0;1;9\right\}\)
Kết hợp ĐKXĐ, ta được: \(a\in\left\{1;9\right\}\)
a) \(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-2}+\dfrac{\sqrt{a}}{\sqrt{a}+2}\right)\cdot\dfrac{a-4}{\sqrt{4a}}\left(dkxd:a\ge0;a\ne4\right)\)
\(=\left[\dfrac{\sqrt{a}\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}+\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\right]\cdot\dfrac{a-4}{2\sqrt{a}}\)
\(=\dfrac{a+2\sqrt{a}+a-2\sqrt{a}}{a-4}\cdot\dfrac{a-4}{2\sqrt{a}}\)
\(=\dfrac{2a}{2\sqrt{a}}\)
\(=\sqrt{a}\)
b) Để \(A-2< 0\) thì: \(\sqrt{a}-2< 0\)
\(\Rightarrow\sqrt{a}< 2\)
\(\Rightarrow a< 4\)
Kết hợp với điều kiện xác định của \(a\), ta được: \(0\le a< 4\)
c) Để \(\dfrac{4}{A+1}\) nguyên thì \(\dfrac{4}{\sqrt{a}+1}\) nguyên
\(\Rightarrow4⋮\sqrt{a}+1\)
\(\Rightarrow\sqrt{a}+1\inƯ\left(4\right)\)
Mà \(\sqrt{a}+1\ge1\forall a\ge0;a\ne4\)
\(\Rightarrow\sqrt{a}+1\in\left\{1;2;4\right\}\)
\(\Rightarrow\sqrt{a}\in\left\{0;1;3\right\}\)
\(\Rightarrow a\in\left\{0;1;9\right\}\)
Kết hợp với điều kiện xác định của \(a\), ta được: \(a\in\left\{0;1;9\right\}\)
\(\text{#}Toru\)

Bạn tham khảo tại đây:
Câu hỏi của Chibi Anime - Toán lớp 6 - Học toán với OnlineMath

a: Để Q là phân số thì n+2<>0
hay n<>-2
b: Thay n=1 vào Q, ta được:
Q=-2/(1+2)=-2/3
Thay n=5 vào Q, ta được:
Q=-2/(5+2)=-2/7
Thay n=-5 vào Q, ta được:
Q=-2/(-5+2)=-2/-3=2/3
a,Vì \(-2,n+2\in Z\Rightarrow Q\) là phân số nếu \(n+2\ne0\left(v\text{ì}0-2=-2\right)\)
b, ta có :
\(n=1\Rightarrow Q=\dfrac{-2}{1+2}=\dfrac{-2}{3}\\ n=5\Rightarrow Q=\dfrac{-2}{5+2}=\dfrac{-2}{7}\\ n=-5\Rightarrow Q=\dfrac{-2}{-5+2}=\dfrac{-2}{-3}\)
vậy ....
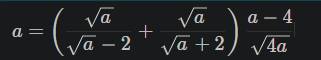 với a ≥ 0, a ≠ 4
với a ≥ 0, a ≠ 4
\(P=\dfrac{8a+15}{4a+1}=\dfrac{4a+4a+1+1+13}{4a+1}=\dfrac{4a+1}{4a+1}+\dfrac{4a+1}{4a+1}+\dfrac{13}{4a+1}=1+1+\dfrac{13}{4a+1}\)
Để P nguyên thì \(\dfrac{13}{4a+1}\in Z\) hay \(4a+1\in U\left\{13\right\}=\left\{\pm1;\pm13\right\}\)
- 4a+1=1 --> a=0
- 4a+1 = -1 --> a= -1/2 ( loại )
- 4a+1 = 13 --> a=3
-4a+1 = -13 --> a= -7/2 ( loại )
Vậy \(a\in Z=\left\{0;3;\right\}\) thì P nhận giá trị nguyên
anh ơi a nguyên