Cho parabol $(P):$ $y = -2 x^2$ và đường thẳng $(d):$ $y = x - m$ (với $m$ là tham số).
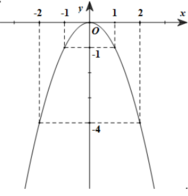
a. Vẽ parabol $(P)$.
b. Tìm tất cả các giá trị của tham số $m$ để đường thẳng $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1$, $x_2$ thỏa mãn điều kiện $x_1 + x_2 = x_1. x_2$.

m = 1