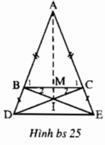
BÀI 1: Cho tam giác ABC. Trên tia đối của tia BA lấy D, trên tia đối của tia CA lấy E sao cho BD = CE = BC. Gọi M là giao điểm của BE và CD đường thẳng qua M song song với tia phân giác của góc BAC cắt AC ở F. Chứng minh rằng AB = CF.
BÀI 2:Cho tam giác đều ABC, điểm M thuộc cạnh BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Vẽ hình bình hành MDNE. CMR: AN // BC.


“““““` ✬ ‘✧ ‘✬
““““` __♜_♜_♜__
“““` `{,,,,,,,,,,,,,,,,,,,,,}
‘“` ✩`{✫//✰//✰//✫}` ✩
‘“` ♖_{♖___♖__♖___.♖}_♖
“` {///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“{//////////////////}
“{_✿__❀_♥_✿_♥_❀__✿_}
““““ * ` ` * ` ` *
‘““““ 0 ` ` 0 ` ` 0
““““ ||___||___||
““ * ` {,,,,,,,,,,,,,,,,,,,} ` *
““ 0 ` {////////} ` 0
‘“`_||_{_______”_____}_||_
“`{///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“`{///////////////}
“`{_____________”________}
cho abc tia phan giac cua goc b cat ac o d tren tia doi cua tia ba lay e sao cho be = bc chung minh bd song song ec cai nay lam sao