a) cho hình thoi ABCD . kẻ hai đường cao AH , AK . Chứng minh rằng AH=AK
b) hình bình hành ABCD có hai đường cao AH,AK bằng nhau . Chứng minh rằng ABCD là hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) Hình vẽ:
Xét hai tam giác vuông \(AHD\) và \(AKB\) ta có:
\(AD=AB\) (cạnh hình thoi)
\(\widehat{D}=\widehat{B}\) (hai góc đối hình thoi)
Do đó: \(\Delta AHD=\Delta AKB\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\) (Đpcm)
b) Hình vẽ:
Cách 1: Ta có: \(\Delta AHD=\Delta AKB\left(g.c.g\right)\)
\(\Rightarrow AD=AK\)
Hình bình hành \(ABCD\) có hai cạnh kề bằng nhau nên là hình thoi (Đpcm)
Cách 2: Ta có: \(\Delta AHC=\Delta AKC\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\)
Hình bình hành \(ABCD\) có một đường chéo là phân giác của một góc nên là hình thoi (Đpcm)

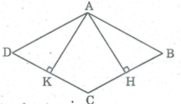
Xét hai tam giác vuông AHC và AKC, ta có:
∠ (AHC) = ∠ (AKC) = 90 0
AH = AK (gt)
AC cạnh huyền chung
Suy ra: ∆ AHC = ∆ AKC (cạnh huyền- cạnh góc vuông)
⇒ ∠ (ACH) = ∠ (ACK) hay ∠ (ACB) = ∠ (ACD)
⇒ CA là tia phân giác ∠ (BCD)
Hình bình hành ABCD có đường chéo CA là đường phân giác nên là hình thoi.

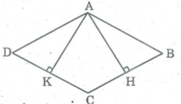
Xét hai tam giác vuông AHB và AKD, ta có:
∠ (AHB) = ∠ (AKD) = 90 0
AB = AD (gt)
∠ B = ∠ D (tính chất hình thoi)
Suy ra: ∆ AHB = ∆ AKD (cạnh huyền, góc nhọn)
⇒ AH = AK

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

Xét ΔAHD vuông tại H và ΔAKB vuông tại K có
AH=AK
góc HAD=góc KAB
=>ΔAHD=ΔAKB
=>AD=AB
=>ABCD là hình thoi

a: BC\(\perp\)BA(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
BA,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
=>BC\(\perp\)SB
=>ΔSBC vuông tại B
Ta có: CD\(\perp\)AD(ABCD là hình vuông)
CD\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AD cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
=>CD\(\perp\)SD
=>ΔSDC vuông tại D
b: Ta có: AH\(\perp\)SB
AH\(\perp\)BC(BC\(\perp\)(SAB))
SB,BC cùng thuộc mp(SBC)
Do đó: AH\(\perp\)(SBC)
=>AH\(\perp\)SC
CD\(\perp\)(SAD)
AI\(\subset\)(SAD)
Do đó: CD\(\perp\)AI
mà AI\(\perp\)SD
và SD,CD cùng thuộc mp(CSD)
nên AI\(\perp\)(SCD)
=>AI\(\perp\)SC
Ta có: AI\(\perp\)SC
AK\(\perp\)SC
AH\(\perp\)SC
=>AI,AK,AH đồng phẳng
c: Xét ΔSAB vuông tại A và ΔSAD vuông tại A có
SA chung
AB=AD
Do đó: ΔSAB=ΔSAD
=>\(\widehat{BSA}=\widehat{DSA}\); SB=SD
Xét ΔSHA vuông tại H và ΔSIA vuông tại I có
SA chung
\(\widehat{HSA}=\widehat{ISA}\)
Do đó: ΔSHA=ΔSIA
=>SH=SI
Xét ΔSBD có \(\dfrac{SH}{SB}=\dfrac{SI}{SD}\)
nên HI//BD
BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó:BD\(\perp\)(SAC)
mà HI//BD
nên HI\(\perp\)(SAC)
mà AK\(\subset\)(SAC)
nên HI\(\perp\)AK
xét \(\Delta\)ACK và ABH có
AB=AC(tc hình thoi)
\(\widehat{AKC}=\widehat{AHB}=90^o\)
\(\widehat{B}=\widehat{C}\)
theo trường hợp cạnh huyền góc nhọn
=>AH=AK (2 cạnh tương ứng)
b)
xét \(\Delta\)AKDvà \(\Delta\)AHB
có\(\widehat{AHB}=\widehat{AK\text{D}}=90^o\)
AH=AK(gt)
\(\widehat{B}=\widehat{D}\)(tính chất HBH)
=>AB=AD(2 cạnh tương ứng)
ABCD là hình thoi vì là HBH có 2 cạnh kề bằng nhau