Bài toán 122
Cho bốn đường tròn tiếp xúc với nhau đôi một như hình vẽ dưới đây. Biết bán kính đường tròn lớn nhất là R, hai đường tròn nhỡ đều có bán kính là R/2. Hãy tính diện tích phần tô màu theo R và ..
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 9 2016
Sáu đường tròn nhỏ có bán kính bằng nhau tiếp xúc ngoài nhau và tiếp xúc trong với đường tròn lớn như hình vẽ dưới đây. Biết bán kính của đường tròn lớn là 2016cm. Hãy tính bán kính của đường tròn nhỏ?
24 tháng 9 2016
Ta dựa trên tính chất của hai đường tròn tiếp xúc trong và tiếp xúc ngoài:
- Hai đường tròn tiếp xúc trong thì điểm tiếp xúc và hai tâm của hai đường tròn thẳng hàng và khoảng cách giữa hai tâm bằng hiệu hai bán kính
- Hai đường tròn tiếp xúc ngoài thì điểm tiếp xúc và hai tâm của hai đường tròn thẳng hàng và khoảng cách giữa hai tâm bằng tổng hai bán kính
Đặt tên các đỉnh như hình vẽ. Gọi bán kính của sáu đường tròn nhỏ là r, bán kính đường tròn to là R.
Dễ thấy các tâm đường tròn nhỏ A,B,C,D,E,F tạo thành lục giác đều có cạnh là 2r.
Tam giác ABK là tam giác cân vì KA = KB = R - r và có góc K bằng 60o (vì bằng 360o / 6 = 60o). Vậy KAB là tam giác đều.
Suy ra KA = AB.
Hay là R - r = 2r.
=> R = 3 r
=> r = R/3 = 2016/3 = 672 cm
Đáp số: bán kính đường tròn nhỏ bằng 672cm.
CM
20 tháng 1 2017
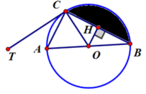
Ta có
T C A ^ = A B C ^ = 30 0 . cos A C B ^ = B C A B = 3 2 ⇒ B C = 3 c m .
Kẻ đường cao OH trong tam giác OBC. Ta có sin O B H ^ = O H O B = 1 2 ⇒ O H = 1 2 c m .
Diện tích tam giác OBC là s 1 = 1 2 . O H . B C = 3 4 c m 2 .
Ta có B O C ^ = 120 0 (vì O B C ^ = B C O ^ = 30 0 ).
Diện tích hình quạt chứa phần tô đen là s 2 = 120 360 . π . R 2 = π 3 c m 2 .
Diện tích phần tô đen là s = s 2 − s 1 = π 3 − 3 4 c m 2 .
Gọi A, B là tâm đường tròn nhở (bán kính R/2), C là tâm đường tròn nhỏ (gọi bán kính là x). Khi đó CA = CB = R/2 + x.
Vậy CAB là tam giác cân ở C. Gọi H là điểm tiếp xúc của hai đường tròn nhỡ. Khi đó HA = HB => H là trung điểm của AB => H chính là tâm đường tròn to.
=> HC = HD - DC = R - x.
Vì CAB cân => CH vừa là trung tuyến, vừa là đường cao. Theo định lý Pitago trong tam giác vuông HAC ta có:
AC2=AH2+HC2
=> (R2 +x)2=(R2 )2+(R−x)2
=> x=R3
Bán kính đường tròn bé nhất x = R/3.
Diện tích phần tô màu bằng diện tích hình tròn to trừ đi tổng ba hình tròn chứa trong hình tròn to, và bằng:
πR2−[π(R2 )2+π(R2 )2+π(R3 )2]=718 πR2
Đáp số: 718 πR2
Xem thêm: