tính 1.2+2.3+3.4+...+99.100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2016
Gọi A là biểu thức ta có:
A = 1.2+2.3+3.4+......+99.100
Gấp A lên 3 lần ta có:
A . 3 = 1.2.3 + 2.3.3 + 3.4.3 + … + 99.100.3
A . 3 = 1.2.3 + 2.3.(4 - 1) + 3.4.( 5 - 2) + … + 99.100. (101 - 98)
A . 3 = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + … + 99.100.101 - 98.99.100
A . 3 = 99.100.101
A = 99.100.101 : 3
A = 33.100.101
A = 333 300
T
24 tháng 11 2016
Đặt biểu thức là A ta có:
A=1.2+2.3+3.4+...+99.100 (1)
Nhân 2 vế của đẳng thức (1) với 3 ta được:
3A=3.(1.2+2.3+3.4+4.5+...+99.100)
3A=1.2.3+2.3.3+3.3.4+4.5.3+...+99.100.3
3A=1.2.3+2.3.(4-1)+3.4.(5-2)+4.5.(6-3)+...+99.100.(101-98)
3A=1.2.3+2.3.4-2.3.1+3.4.5-2.3.4+4.5.6-4.5.3+...+99.100.101-99.100.98
3A=99.100.101
3A=999900
A=999900:3=333300
2 tháng 2 2017
A = 1.2+2.3+3.4+......+99.100
Gấp A lên 3 lần ta có:
A . 3 = 1.2.3 + 2.3.3 + 3.4.3 + … + 99.100.3
A . 3 = 1.2.3 + 2.3.(4 - 1) + 3.4.( 5 - 2) + … + 99.100. (101 - 98)
A . 3 = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + … + 99.100.101 - 98.99.100
A . 3 = 99.100.101
A = 99.100.101 : 3
A = 33.100.101
A = 333 300
LN
2 tháng 2 2017
Đặt A = 1.2 + 2.3 + 3.4 + ...+99.100
=> 3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + 99.100.3
=> 3A = 1.2.3 + 2.3.(4-1) + 3.4.(5-2) + ... + 99.100.(101-98)
=> 3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + 4.5.6 - 3.4.5 + ... + 99.100.101-98.99.100
=> 3A = 1.2.3 - 1.2.3 + 2.3.4 - 2.3.4 + 3.4.5 - 3.4.5 + ... + 99.100.101
=> 3A = 99.100.101
=> 3A = 999900
=> A = 999900 : 3
=> A = 333300
Vậy A = 333300
PT
Phạm Trần Hoàng Anh
CTVHS
22 tháng 7 2021
`S = 1.2 + 2.3 + 3.4 + 4.5 + ... + 99.100.`
`3S = 1.2.3 + 2.3.(4-1) + 3.4.(5-4) + 4.5.(6-3) + ... + 99.100.(101-98)`
`3S = 1.2.3 + 2.3.4-1.2.3 + 3.4.5-4.5.6 + 4.5.6-3.4.5 + ... + 99.100.101-98.99.100`
`3S = 99.100.101`
`S = 33.100.101`
`S = 333300`
22 tháng 7 2021
3S=1.2(3-0)+2.3(4-1)+.....+99.100(101-98)
=1.2.3-0.1.2+2.3.4-1.2.3+4.5.6-2.3.4+....+99.100.101-98-99-100
=99.100.101
S=33.100.101
=333300
13 tháng 5 2016
Đặt A= 1.2+2.3 +.......+99.100
3A= 1.2.3+2.3.4+3.4.3 +......+ 99.100.3
3A= 1.2. (3 - 0) + 2.3.(4 - 1) +3.4. (5 - 2)....... . 99.100. (101 - 98)
3A = (1.2.3 + 2.3.4 + 3.4.5 +...... + 99.100.101) - (0.1.2 + 1.2.3 + 2.3.4 +.......+ 98.99.100)
3A = 99.100.101 - 0.1.2
3A = 999900 - 0
3A= 999900
A= 999900 : 3
A = 333300
TN
13 tháng 5 2016
Đặt A= 1.2+2.3 +.......+99.100
3A= 1.2.3+2.3.4+3.4.3 +......+ 99.100.3
3A= 1.2. (3 - 0) + 2.3.(4 - 1) +3.4. (5 - 2)....... . 99.100. (101 - 98)
3A = (1.2.3 + 2.3.4 + 3.4.5 +...... + 99.100.101) - (0.1.2 + 1.2.3 + 2.3.4 +.......+ 98.99.100)
3A = 99.100.101 - 0.1.2
3A = 999900 - 0
3A= 999900
A= 999900 : 3
A = 333300
nguồn:câu hỏi tương tự
MH
3 tháng 2 2016
S = 1.2 + 2.3 + 3.4 + ... + 99.100
=> 3S = 1.2.3 + 2.3.3 + 3.4.3 + ... + 99.100.3
=> 3S = 1.2.(3 - 0) + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + 99.100.(101 - 98)
=> 3S = 1.2.3 - 0 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ... + 99.100.101 - 98.99.100
=> 3S = 99.100.101
=> S = \(\frac{99.100.101}{3}=333300\)
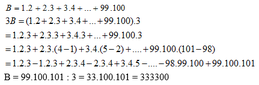
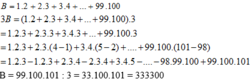
Đặt S=1.2+2.3+3.4+...+99.100
=>3S=1.2.(3-0)+2.3.(4-1)+3.4.(5-2)+...+99.100.(101-98)
=>3S=1.2.3-0.1.2+2.3.4-1.2.3+3.4.5-2.3.4+...+99.100.101-98.99.100
=>S=\(\frac{99.100.101}{3}\)
=>S=333 300
carm own bn nha