cho hình tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB=AC=AD=5cm gọi M là trung điểm BC a) chứng minh BC vuông góc ADM b) tính khoảng cách từ điểm A đén BCD C) tính góc giữa đường thẳng DM và mặt phẳng ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Chọn hệ trục tọa độ Oxy
![]()
A D = 2 a tan 60 o = 2 a 3
Từ M kẻ MH song song với AC ta có MH =a
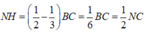
![]()
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1
Vậy khoảng cách từ
P
(
0
;
4
a
;
0
)
đến (BCD) là:
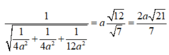

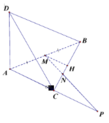
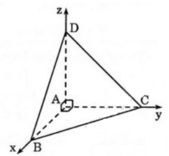
Chọn hệ trục tọa độ Oxyz. Có O = A, AB = Ox, AC = Oy, AD = Oz, AD = 2 α tan 60 o = 2 a 3 , N H = 1 2 - 1 3 B C = 1 6 B C = 1 2 N C
Từ M kẻ MH song song với AC ta có MH = a; CP = 2MH = 2a ⇒ AP = 4a
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1 . Vậy khoảng cách từ P ( 0;4a;0 ) đến (BCD) là:
1 1 4 a 2 + 1 4 a 2 + 1 12 a 2 = a 12 7 = 2 a 21 7
Đáp án cần chọn là A

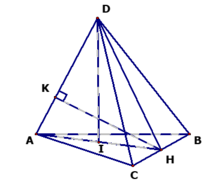
CMR: BC ⊥ (ADH) và DH = a.
● Δ ABC đều, H là trung điểm BC nên AH BC, AD BC
⇒ BC ⊥ (ADH) ⇒ BC ⊥ DH.
⇒ DH = d(D, BC) = a

Đáp án B
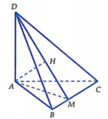
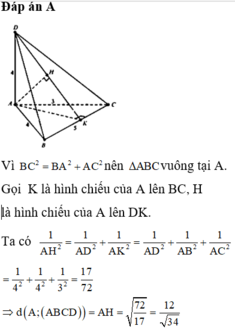
Ta có A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong (ABC) kẻ AM vuông góc tại M ⇒ 1 A M 2 = 1 A B 2 + 1 A C 2
Trong (DAM) kẻ A H ⊥ D M tại H.
Ta có
D A ⊥ B C ; A M ⊥ B C ⇒ D A M ⊥ B C ⇒ D A M ⊥ D B C
D A M ⊥ D B C D A M ∩ D B C = D M A H ⊂ D A M ; A H ⊥ D M ⇒ A H ⊥ D B C
⇒ d A ; D B C = A H
Tam giác DAM vuông tại A có AH là đường cao
⇒ 1 A H 2 = 1 A M 2 + 1 A D 2 = 1 A B 2 + 1 A C 2 + 1 A D 2 = 1 3 2 + 1 4 2 + 1 4 2 = 17 72 ⇒ A H = 12 34

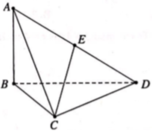
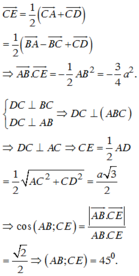
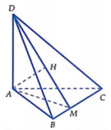


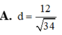
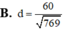
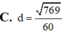
a.
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)