cho 6 số thực a1<a2<a3<a4<a5<a6. Chứng minh rằng phương trình (x-a1)(x-a3)(x-a5)+(x-a2)(x-a4)(x-a6)=0 có đúng 3 nghiệm phân biệt.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
1
28 tháng 10 2020
Đặt \(A = a_{1} + a_{2} + \dots + a_{n}; B = a_{1}^3 + a_{2}^3 + \dots + a_{n}^3 \)
Ta có \(a_n^3-a_n=a_n\left(a_n^2-1\right)=a_n\left(a_n-1\right)\left(a_n+1\right)⋮6\)(tích ba số nguyên liên tiếp sẽ có một số chia hết cho 2, một số chia hết cho 3)
Ta có \(B-A=a_1\left(a_1-1\right)\left(a_1+1\right)+a_2\left(a_2-1\right)\left(a_2+1\right)+...+a_n\left(a_n-1\right)\left(a_n+1\right)\)
Suy ra \(B-A⋮6\)
=> A,B cùng chia hết cho 6 hoặc cùng không chia hết cho 6
=> nếu \(A⋮6\)thì \(B⋮6\)
=>ĐPCM
MC
1
TN
7 tháng 9 2017
Ko mất tính tổng quát giả sử \(a_1=\text{max}\left\{a_2;a_3;a_4;a_5\right\}\).
Áp dụng BĐT AM-GM ta có:
\(a_1a_2+a_2a_3+a_3a_4+a_4a_5\le a_1\left(a_2+a_3+a_4+a_5\right)\)
\(\le\frac{\left(a_1+a_2+a_3+a_4+a_5\right)^2}{4}=\frac{1}{4}\)
Xảy ra khi có 2 số bằng \(\frac{1}{2}\) và 3 số còn lại bằng 0
VT
4 tháng 10 2018
Đáp án B
+ Ta có
tan φ = a 1 sin φ 1 + a 2 sin φ 2 a 1 cos φ 1 + a 2 cos φ 2 ⇔ 1 3 = a 1 + 3 2 a 2 - 1 2 a 2 ⇒ a 1 = - 1 2 3 + 3 2 a 2
⇔ a 1 = - 2 3 a 2 .
-> Với a 1 và a 2 trái dấu nhau -> độ lệch pha của hai dao động cos Δ φ = - cos 2 π 3 - π 2 = - 3 2 .
+ Áp dụng công thức tổng hợp dao động, ta có:
25 = a 1 2 + a 2 2 - 3 a 1 a 2 thay a 1 = - 2 3 a 2 , ta thu được phương trình a 2 2 3 = 25 ⇒ a 2 = ± 5 3 ⇒ a 1 a 2 = - 50 3 .
MC
0
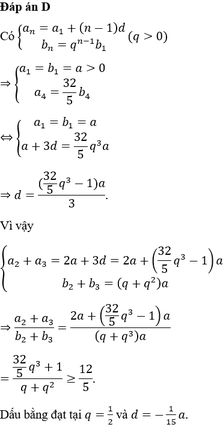
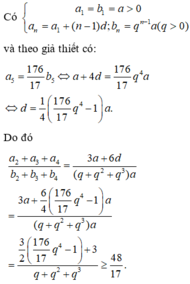
Đặt \(f\left(x\right)=\left(x-a_1\right)\left(x-a_3\right)\left(x-a_5\right)+\left(x-a_2\right)\left(x-a_4\right)\left(x-a_6\right)\)
\(f\left(a_1\right)=\left(a_1-a_2\right)\left(a_1-a_4\right)\left(a_1-a_6\right)< 0\)
\(f\left(a_2\right)=\left(a_2-a_1\right)\left(a_2-a_3\right)\left(a_2-a_5\right)>0\)
\(f\left(a_4\right)=\left(a_4-a_1\right)\left(a_4-a_3\right)\left(a_4-a_5\right)< 0\)
\(f\left(a_6\right)=\left(a_6-a_1\right)\left(a_6-a_3\right)\left(a_6-a_5\right)>0\)
\(\Rightarrow f\left(x\right)\) có nghiệm thuộc các khoảng \(\left(a_1,a_2\right);\left(a_2,a_4\right);\left(a_4,a_6\right)\)
mà bậc cao nhất của f(x) là 3 nên f(x) có tối đa 3 nghiệm
=> dpcm