Cho tam giác ABC cân tại A , trung tuyến AM. Qua điểm B vẽ đường thẳng song song với đường thẳng AC cắt đường thẳng AM tại điểm D
a)Chứng minh : tam giác ABC = tam giác DMB
b)Chứng minh : AB=BD
c)Gọi P là trung điểm của đoạn thẳng AB , đoạn thẳng PD cắt đoạn thẳng BC tại O. Trên tia đối của tia PO lấy điểm N sao cho PN=PO. Chứng minh điểm O là trọng tâm của tam giác ABD và NA=2OM


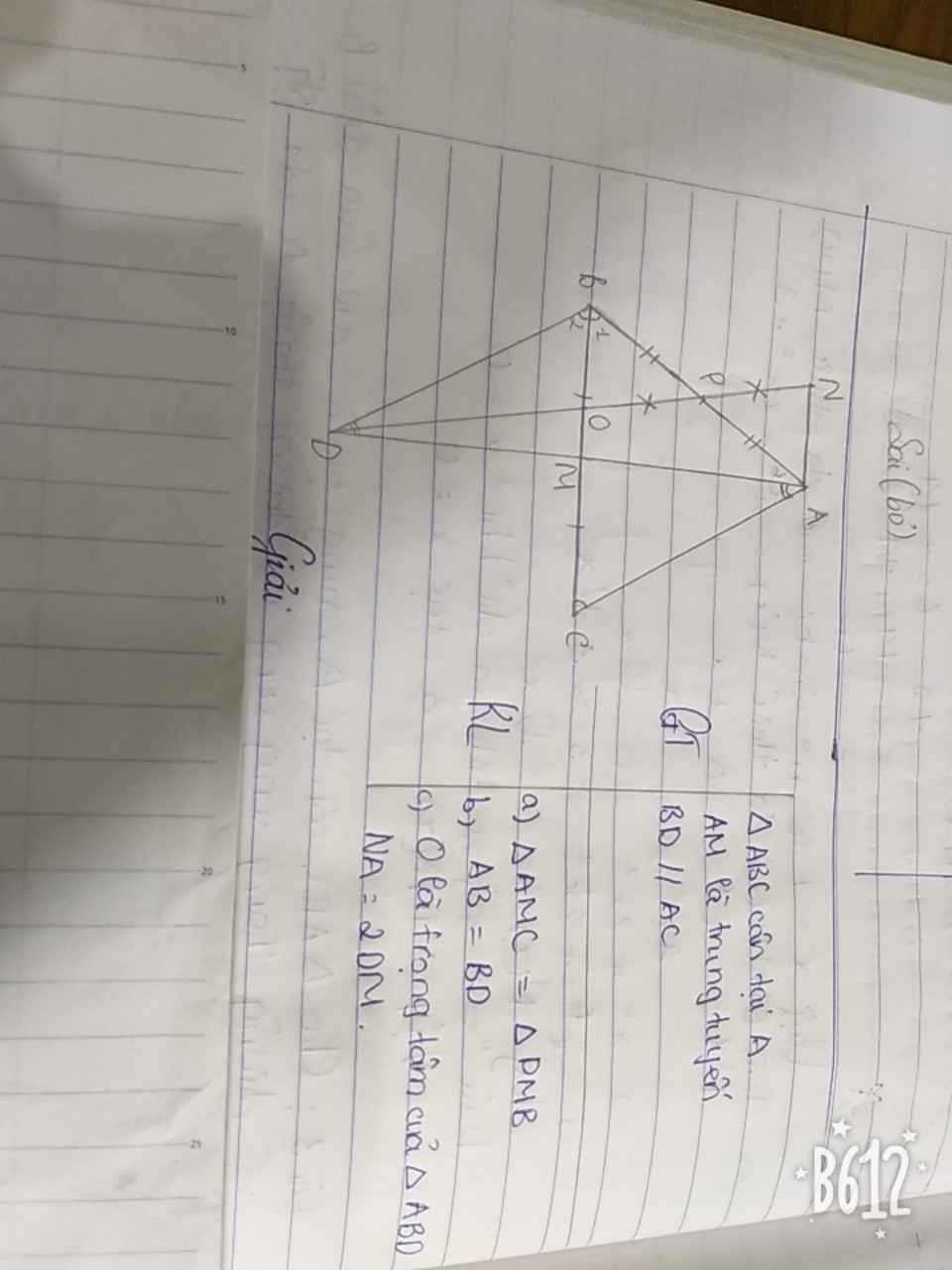
a: Sửa đề ΔAMC
Xét ΔAMC và ΔDMB có
góc MCA=góc MBD
MC=MB
góc AMC=góc DMB
=>ΔAMC=ΔDMB
b: ΔAMC=ΔDMB
=>AC=BD
=>BD=AB
c: Xét ΔBAD có
BM,DP là trung tuyến
BM cắt DP tại O
=>O là trọng tâm