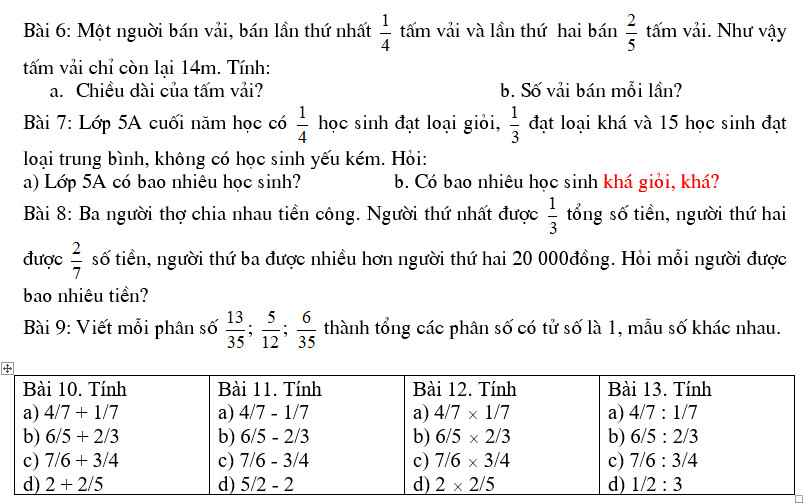
Ai giúp mình bài 6,7 vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 6.
a)Công suất ấm: \(P=\dfrac{A}{t}=\dfrac{900\cdot1000}{10\cdot60}=1500W\)
Dòng điện qua ấm: \(I=\dfrac{P}{U}=\dfrac{1500}{220}=\dfrac{75}{11}A\)
Điện trở dây nung: \(R=\dfrac{U}{I}=\dfrac{220}{\dfrac{75}{11}}=\dfrac{484}{15}\Omega\)
b)Điện năng tiêu thụ trong 1 tháng (30 ngày):
\(T=900\cdot1000\cdot30\cdot3600=9,72\cdot10^{10}J=27000kWh\)
Tiền điện phải trả: \(T=27000\cdot1500=40500\left(k.đồng\right)\)
c)Công suất tiêu thụ thực:
\(P=UI=\dfrac{U^2}{R}=\dfrac{110^2}{\dfrac{484}{15}}=375W\)
Bài 7.
CTM: \(\left(Đ_1ntR_b\right)//Đ_2\)
\(R_1=\dfrac{U_{Đ1}^2}{P_{Đ1}}=\dfrac{10^2}{2}=50\Omega;I_{Đ1đm}=\dfrac{P_{Đ1}}{U_{Đ1}}=\dfrac{2}{10}=0,2A\)
\(R_2=\dfrac{U^2_{Đ2}}{P_{Đ2}}=\dfrac{12^2}{3}=48\Omega;I_{Đ2đm}=\dfrac{P_{Đ2}}{U_{Đ2}}=\dfrac{3}{12}=0,25A\)
Để đèn 1 sáng bình thường \(\Rightarrow I_b=I_{Đ1đm}=0,2A\)
\(R_{Đ1+b}=\dfrac{12}{0,2}=60\Omega\)
\(R_b=60-R_{Đ1}=60-50=10\Omega\)


Gọi số học sinh lớp 7a , 7b lần lượt là a ; b \(\left(a;b\inℕ^∗\right)\)
Theo bài ra ta có :
\(\frac{a}{6}=\frac{b}{7}\)
\(\Rightarrow\frac{a}{6}=\frac{2a}{12}=\frac{b}{7}\)và \(2a-b=25\)
ADTCDTSBN , ta có :
\(\frac{a}{6}=\frac{2a}{12}=\frac{b}{7}=\frac{2a-b}{12-7}=\frac{25}{5}=5\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{6}=5\\\frac{b}{7}=5\end{cases}\Rightarrow\hept{\begin{cases}a=5.6=30\\b=5.7=35\end{cases}}}\)
Vậy ...

1,2 + 2,3 + 3,4 - 4,5 + 5,6 - 6,7 + 7,8 - 8,9 + 9,1 = 9,3


2:
a: |2x-3|=7
=>2x-3=7 hoặc 2x-3=-7
=>x=5(loại) hoặc x=-2(nhận)
Khi x=-2 thì \(B=\dfrac{-2+1}{2\cdot\left(-2\right)^2-10\cdot\left(-2\right)}=\dfrac{-1}{2\cdot4+20}=\dfrac{-1}{28}\)
b: \(A=\dfrac{15-x+2x-10}{\left(x-5\right)\left(x+5\right)}=\dfrac{1}{x-5}\)
c: P=A:B
\(=\dfrac{1}{x-5}\cdot\dfrac{2x\left(x-5\right)}{x+1}=\dfrac{2x}{x+1}\)
P>2
=>P-2>0
=>(2x-x-1)/(x+1)>0
=>(x-1)/(x+1)>0
=>x>1 hoặc x<-1




 ai giúp mình bài 2 vs =))))
ai giúp mình bài 2 vs =))))
6.
Do \(AA'\perp\left(ABCD\right)\) (t/c hình hộp chữ nhật)
Mà \(AA'\in\left(ACC'A'\right)\)
\(\Rightarrow\left(ACC'A'\right)\perp\left(ABCD\right)\Rightarrow\) góc giữa (ACC'A') avf (ABCD) bằng 90 độ
b.
Từ H kẻ AH vuông góc BD (H thuộc BD)
Do \(AA'\perp\left(ABCD\right)\Rightarrow AA'\perp BD\)
\(\Rightarrow BD\perp\left(A'AH\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BD\perp AH\\BD\perp A'H\end{matrix}\right.\)
Mà \(BD=\left(A'BD\right)\cap\left(ABCD\right)\Rightarrow\widehat{AHA'}\) là góc giữa (A'BD) và (ABCD)
\(AH=\dfrac{AB.AD}{\sqrt{AB^2+AD^2}}=\dfrac{bc}{\sqrt{b^2+c^2}}\)
\(\Rightarrow tan\widehat{AHA'}=\dfrac{AA'}{AH}=\dfrac{a\sqrt{b^2+c^2}}{bc}\)
7.
Kẻ \(AI\perp CM\Rightarrow\widehat{IAM}=\widehat{BCM}\) (góc có cạnh tương ứng vuông góc)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{BC^2+\left(\dfrac{AB}{2}\right)^2}=2a\)
\(\Rightarrow AI=AM.cos\widehat{IAM}=\dfrac{AB}{2}.cos\widehat{BCM}=\dfrac{AB}{2}.\dfrac{BC}{CM}=\dfrac{a\sqrt{3}}{2}\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp CI\\CI\perp AI\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CI\perp\left(SAI\right)\Rightarrow\left\{{}\begin{matrix}CI\perp SI\\CI\perp AI\end{matrix}\right.\)
Mà \(CI=\left(SMC\right)\cap\left(ABC\right)\Rightarrow\widehat{SIA}\) là góc giữa (SMC) và (ABC)
\(tan\widehat{SIA}=\dfrac{SA}{AI}=\dfrac{4\sqrt{3}}{3}\Rightarrow\widehat{SIA}\approx66^035'\)