Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
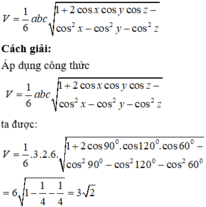

Theo đề bài, ta có: \(\widehat{B}+\widehat{C}+\widehat{B}+\widehat{D}=200^0+180^0\)
\(\Leftrightarrow2\widehat{B}+\left(\widehat{C}+\widehat{D}\right)=380^0\)
\(\Leftrightarrow2\widehat{B}=380^0-120^0=260^0\)
\(\Rightarrow\widehat{B}=130^0\Rightarrow\widehat{C}=70^0,\widehat{D}=50^0\)
Mỗi tứ giác đều được tạo thành từ \(2\) tam giác phân biệt nên tổng các góc trong một tứ giác là \(360^0\).
Do đó, \(\widehat{A}=360^0-130^0-70^0-50^0=110^0\)
Vậy: ...
( Có hết trên kia rồi, bạn tự bổ sung từ vậy )
\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)