Giúp mik vs ạ...
Cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NC
0
KY
19 tháng 8 2021
beautifully
excitedly
interesting
collected
arrangements
peacefully
excited
different
6 tháng 8 2021
a,\(x^2-7x+6=x^2-x-6x+6\)
\(=x\left(x-1\right)-6\left(x-1\right)\)
\(=\left(x-6\right)\left(x-1\right)\)
6 tháng 8 2021
a) x2-7x+6=(x2-x)-(6x-6)=x(x-1)-6(x-1)=(x-6)(x-1)
b) x2-6x+3=(x2-6x+9)-6=(x-3)2-\(\sqrt{6^2}\)=(x-3-\(\sqrt{6}\))(x-3+\(\sqrt{6}\))
c) x2-4x+3=(x2-x)-(3x-3)=x(x-1)-3(x-1)=(x-3)(x-1)
d) 3x2-5x+2=(3x2-3x)-(2x-2)=3x(x-1)-2(x-1)=(3x-2)(x-1)
e) 7x2-x-6=(7x2-7x)+(6x-6)=7x(x-1)+6(x-1)=(7x+6)(x-1)
f) 3x2-5x-8=(3x2+3x)-(8x+8)=3x(x+1)-8(x+1)=(3x-8)(x+1)
g) x2-6x+5=(x2-x)-(5x-5)=x(x-1)-5(x-1)=(x-5)(x-1)
h) x2-2x-3=(x2-2x+1)-4=(x-1)2-22=(x-1-2)(x-1+2)=(x-3)(x+1)
i) x2-x-12=(x2+3x)-(4x+12)=x(x+3)-4(x+3)=(x-4)(x+3)
M
1
4 tháng 4 2023
27. unforgetable
câu 31 đổi thành ...if I can give him his guide....
câu 32 thiếu on trong turned on và đổi thành has been turned on vì câu gốc là HTHT
câu 33 rút gọn mệnh đề ok
câu 34 hơi phân vân nhưng mình thấy đúng
DT
Đỗ Thanh Hải
CTVVIP
5 tháng 7 2021
1 are
2 am
3 is
4 are
5 are
6 are
7 is
8 is
9 is
10 are
IV
1 is writing
2 are losing
3 is having
4 is staying
5 am not lying
6 is always using
7 are having
8 Are you playing
9 are not touching
10 Is - listening
11 Is- winning
12 am not staying
13 is not working
14 is not reading
15 isn't raining
16 am not listening
17 Are they making
18 Are you doing
19 Is - sitting
20 is - doing
21 are-putting
22 are-wearing
23 is-studying
5 tháng 7 2021
2, am
3, is
4,are
5,are
6,are
7,is
8,is
9,is
10,are
IV
1,2,7 OK
3,is having
4,has stayed
5,am not lying
6,always uses
8,Are-playing
9,not to touch
10,Is-listening
11,Are-winning
12,am not staying
13,isn't working
14,isn't reading
15,isn't raining
16,am not listening
17,Are-making
18,Are-doing
19,Is-sitting
20,is-doing
21,do-putting
22,do-wear
23,is-studying
AH
Akai Haruma
Giáo viên
31 tháng 12 2021
Lời giải:
ĐKĐB $\Rightarrow \frac{2}{c}=\frac{a+b}{ab}\Rightarrow c(a+b)=2ab$
Khi đó:
$\frac{a}{b}-\frac{a-c}{c-b}=\frac{a(c-b)-b(a-c)}{b(c-b)}=\frac{ac-ab-ab+bc}{b(c-b)}=\frac{c(a+b)-2ab}{b(c-b)}=\frac{2ab-2ab}{b(c-b)}=0$
$\Rightarrow \frac{a}{b}=\frac{a-c}{c-b}$ (đpcm)
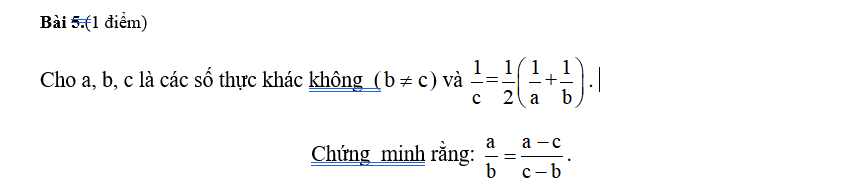
Đéo *Thảo Lee*