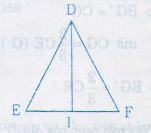
Bài 1 Cho tam giác DEF cân tại D với đường trung tuyến DI
a/ Chứng minh : ∆ DEI = ∆DFI
b/ Các góc DIE và góc DIF là những góc gì ?
c/ Biết DI = 12cm , EF = 10cm . Hãy tính độ dài cạnh DE.
Bài 2 Cho DABC biết AB = 3cm, AC = 4cm, BC = 5cm. Trên tia đối của tia AC lấy điểm D sao cho
AD =AC
a) Chứng minh tam giác ABC vuông
b) Chứng minh DBCD cân
c)Gọi E là trung điểm của BD, CE cắt AB tại O. Tính OA, OC
Bài 3: (Đề Đông Hà năm học 2015 - 2016)
Cho tam giác ABC vuông tại A và đường phân giác BD. Kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng:
a) ∆ ABD = ∆ EBD
b) BD 
AE
c) BD đi qua trung điểm của CF
Bài 4:
Cho tam giác ABC cân tại A, vẽ AH vuông góc với BC tại H. Biết AB=5cm, BC= 6cm.
a) Chứng minh BH =HC.
b) Tính độ dài BH, AH.
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng A, G, H thẳng hàng.
d) Chứng minh góc ABG= góc ACG
Bài 5.
Cho DABC có góc C = 900 ; BC = 3cm; CA = 4cm. Tia phân giác BK của góc ABC (K Î CA); từ K kẻ
KE ^ AB tại E.
a) Tính AB.
b) Chứng minh BC = BE.
c) Tia BC cắt tia EK tại M. So sánh KM và KE.
d) Chứng minh CE // MA
Bài 6:
Cho tam giác ABC vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (H 
BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:
a) Tam giác ABE=tam giác HBE
b) BE là đường trung trực của đoạn thẳng AH.
c) EK = EC.
d) AE < EC.
4:
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
b: BH=CH=6/2=3cm
AH=căn 5^2-3^2=4cm
c: Xét ΔABC có
AH là trung tuyến
G là trọng tâm
=>A,G,H thẳng hàng
d: Xét ΔABG và ΔACG có
AB=AC
góc BAG=góc CAG
AG chung
=>ΔABG=ΔACG
=>góc ABG=góc ACQ