tính cạnh góc vuông của 1 tam giác vuông biết cạnh huyền = 13 và cạnh góc vuông kia = 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm

Giả sử ∆ABC có ∠A =90o, BC = 13 cm, AC = 12cm
Theo định lý pitago ta có: BC2 = AB2 + AC2
Suy ra: AB2=BC2-AC2=132-122=25
Vậy AB = 5 cm
Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm

LẤY 13^2- 12^2= 169-144=25 Vậy cạnh góc vuông còn lại sẽ = 5
Giả sử ∆ABC có \(\widehat{A}\)= \(90^0\), BC = 13 cm, AC = 12cm
Theo định lý Pitago ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
Hay \(AC^2=13^2-12^2\)
\(AC^2=169-144\)
\(AC^2=25\)
\(AC=\sqrt{25}\)
\(AC=5cm\)

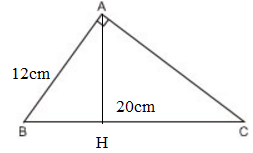
Gọi 2 tam giác đó lần lượt là `\DeltaABC,\DeltaA'B'C'`
Cạnh góc vuông là cạnh huyền của 2 tam giác lần lượt là `AB,BC` và `A'B',B'C`
Xét tam giác `\DeltaABC` và `\DeltaA'B'C'`:
`(AB)/(BC)=(A'B')/(B'C')`
`\hat{BAC}=\hat{B'A'C'}=90^o`
`=>\DeltaABC~\DeltaA'B'C'`

Gọi x là độ dài cạnh góc vuông nhỏ
Độ dài cạnh góc vuông lớn là: x+1
Theo đề, ta có phương trình:
\(x^2+\left(x+1\right)^2=25\)
\(\Leftrightarrow2x^2+2x+1-25=0\)
\(\Leftrightarrow x^2+x-12=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\left(loại\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
Chu vi tam giác vuông đó là:
\(3+4+5=12\left(m\right)\)
Gọi cạnh góc vuông nhỏ hơn của tam giác vuông đó là a(m)(a>0)
Theo đề ra, ta có:
\(a^2+\left(a+1\right)^2=25\\ \Rightarrow a^2+a^2+2a+1=25\\ \Rightarrow2a^2+2a=24\\ \Rightarrow a\left(a+1\right)=12=3.4\\ \Rightarrow a=3\)
Chu vi tam giác đó là:
3 + 3 + 1 + 5 = 12(m)
Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13cm, cạnh góc vuông kia bằng 12cm ?

Đặt tên cho \(\Delta\) này là \(\Delta\)ABC, ta có:
AB & BC là cạnh góc vuông.
AC là cạnh huyền.
Áp dụng định lý py-ta-go vào \(\Delta\)ABC, ta có:
AC2 = AB2 + BC2
132 = 122 + BC2
169 = 144 + BC2
BC2 = 169 - 144 = 25
BC = \(\sqrt{25}\) = 5cm.
Vậy cạnh BC = 5cm hay cạnh góc vuông còn lại của \(\Delta\) = 5cm.
13 12 A B C
Giả sử ∆ABC có ˆA=90∘, BC = 13cm, AC = 12cm
Theo định lý Pytago, ta có: BC2=AB2+AC2
Suy ra: AB2=BC2−AC2=132−122=252
Vậy AB = 5 (cm)
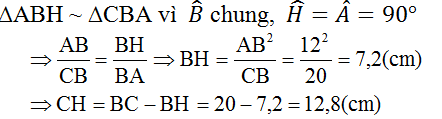
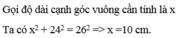
gọi cạnh cần tìm là a
áp dụng định lí py-ta-go có
a^2=13^2+12^2
a^2=313
a= căn bậc hai của 313