Cho tam giác ABC có A=80°,trực tâm H . Gọi M là điểm đối xứng với H qua BC.
a/ Chứng minh ΔBHC=ΔBMC
b/ Tính góc BMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 9 2016
a) Gọi O là giao điểm của HM và BC.
Ta có: M là điểm đối xứng của H qua BC (gt)
=> BC là đường trung trực của HM.
Ta có: BO là đường cao của tam giác BHM (BC vuông góc HM).
BO là đường trung tuyến của tam giác BHM (HO=MO).
=> Tam giác BHM cân tại B (t/c).
=> BH = BM (t/c)
=> CM = CH (chứng minh tương tự)
Xét tam giác BHC và tam giác BMC, có:
* BC là cạnh chung (gt)
* BH = BM (cmt)
* CH = CM (cmt)
=> Tam giác BHC = Tam giác BMC (c.c.c) (đpcm).
b) Gọi F là giao điểm của đường cao BF với AC.
Gọi G là giao điểm của đường cao CG với AB.
Xét tam giác ABF vuông tại F, có:
Góc BAC + Góc BFA + Góc ABF = 180 độ (tổng 3 góc của 1 tam giác)
80 độ + 90 độ + Góc ABF = 180 độ
Góc ABF = 180 độ - 80 độ - 90 độ
Góc ABF = 10 độ
Xét tam giác BGH vuông tại G, có:
Góc BGH + Góc BHG + Góc GBH = 180 độ (tổng 3 góc của 1 tam giác)
90 độ + 10 độ + Góc BHG = 180 độ
Góc BHG = 180 độ - 90 độ - 10 độ
Góc BHG = 80 độ
Mà góc BHG = góc CHF (đối đỉnh)
Nên góc CHF = 80 độ
Ta có: góc BHC + góc CHF = 180 độ ( kề bù)
góc BHC + 80 độ = 180 độ
góc BHC = 180 độ - 80 độ
góc BHC = 100 độ
Ta có: góc BHC = góc BMC (tam giác BHC = tam giác BMC)
Mà góc BHC = 100 độ (cmt)
Nên góc BMC = 100 độ (đpcm).
7 tháng 10 2021
a: Ta có: M và H đối xứng nhau qua BC
nên BC là đường trung trực của MH
Suy ra: BM=BH; CM=CH
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC
7 tháng 11 2021
a: Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC
7 tháng 10 2021
a: Ta có: M và H đối xứng nhau qua BC
nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC
CM
25 tháng 5 2019
a) Chứng minh được DBHC = DBMC (c.c.c).
b) Gọi {C'} = CH Ç AB. Sử dụng định lý tổng 4 góc trong tứ giác AB'HC' ta tính được B ' H C ' ^ = 120 0
Ta có B ' H C ' ^ = B H C ^ (đối đỉnh) và B C H ^ = B M C ^ ( d o △ B H C = △ B M C ) ⇒ B M C ^ = 120 0
18 tháng 7 2021
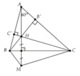
a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM(cmt)
CH=CM(cmt)
BC chung
Do đó: ΔBHC=ΔBMC(c-c-c)
CM
16 tháng 5 2017
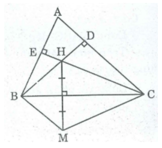
Gọi giao điểm BH với AC là D, giao điểm của CH và AB là E, H là trực tâm của ΔABC
⇒ BD ⊥ AC, CE ⊥ AB
Xét tứ giác ADHE, ta có:
∠ (DHE) = 360 0 – ( ∠ A + ∠ D + ∠ E ) = 360 0 - 60 0 + 90 0 + 90 0 = 120 0
∠ (BHC) = ∠ (DHE)(đối đỉnh)
∆ BHC = ∆ BMC (chứng minh trên)
⇒ ∠ (BMC) = ∠ (BHC)
Suy ra: ∠ (BMC) = ∠ (DHE) = 120 0
CM
26 tháng 10 2017
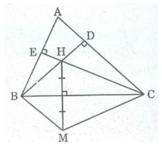
Vì M đối xứng với H qua trục BC
⇒ BC là đường trung trực của HM
⇒ BH = BM (t/chất đường trung trực)
CH = CM (t/chất đường trung trực)
Xét tam giác BHC và tam giác BMC có:
BC chung
BH= BM ( chứng minh trên)
CH = CM (chứng minh trên)
Suy ra: ∆ BHC = ∆ BMC (c.c.c)