Một vật sáng AB có dạng mũi tên cao 1 cm .Đặt trước và cách thấu kính hội tụ một đoạn d = 4 cm .Thấu kính có tiêu cự f = 3 cm
a) vẽ ảnh A'B' của AB qua thấu kính
b) Dựa vào hình vẽ nêu tính chất ảnh
c) Xác định vị trí và độ lớn của anh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2022
Câu 1.
Khoảng cách từ ảnh đến thấu kinh:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{d'}=\dfrac{1}{d}+\dfrac{1}{f}=\dfrac{1}{30}+\dfrac{1}{15}=\dfrac{1}{10}\)
\(\Rightarrow d'=10cm\)
Độ cao vật: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{18}=\dfrac{30}{10}\Rightarrow h=54cm\)
Câu 2.
Bạn tự vẽ hình nha!!!
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{60}=\dfrac{1}{d'}-\dfrac{1}{40}\Rightarrow d'=24cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{40}{24}\Rightarrow h'=1,2cm\)
VT
24 tháng 4 2017
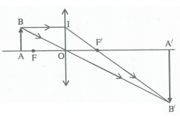
a) Dựng ảnh của vật qua thấu kính.
+ Qua B kẻ tia tới BI // với trục chính, thì tia ló qua I và tiêu điểm ảnh F’.
+ Xuất phát từ B kẻ tia qua quang tâm O, tia này giao với tia IF’ tại B’, B’ là ảnh của B.
+ Từ B hạ vuông góc xuống trục chính cắt trục chính tại A’.
+ Vậy A’B’ là ảnh của AB cần dựng.
b) Áp dụng công thức thấu kính ta có:
H9
HT.Phong (9A5)
CTVHS
6 tháng 5 2023
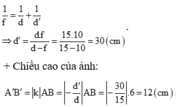
Ta có:
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{15}{OA'}\left(1\right)\)
\(\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}=\dfrac{OF'}{OA'-OF'}=\dfrac{30}{OA'-30}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{15}{OA'}=\dfrac{30}{OA'-30}\)
\(\Leftrightarrow15\left(OA'-30\right)=30OA'\)
\(\Leftrightarrow15OA'-450=30OA'\)
\(\Leftrightarrow-450=30OA'-15OA'\)
\(\Leftrightarrow-450=15OA'\)
\(\Leftrightarrow OA'=\dfrac{-450}{15}=-30\left(cm\right)\)
Vậy khoảng cách từ ảnh đến thấu kính là: -30cm
a,
b) Ảnh thật , ngược chiều vật , lớn hơn vật
c)
Áp dụng công thức thấu kính ta có:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(d'=\dfrac{d.f}{d-f}=\dfrac{4.3}{4-3}=12\left(cm\right)\)
Độ lớn của ảnh:
\(k=-\dfrac{d'}{d}=-3\Rightarrow A'B'=\left|k\right|.AB=3\left(cm\right)\)
you lớp ...... mà làm đc bài này :) có lẽ nào