giải chi tiết cho mình câu này nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều dài của mảnh đất là x (25<x<50)
Chiều rộng của mảnh đất là: \(50-x\) (m)
Diện tích mảnh đất ban đầu: \(x\left(50-x\right)\)
Chiều dài và chiều rộng mảnh đất sau khi mở lối đi lần lượt là: \(x-2\) và \(48-x\)
Diện tích phần đất trồng rau: \(\left(x-2\right)\left(48-x\right)\)
Ta có pt:
\(\left(x-2\right)\left(48-x\right)=\dfrac{84}{100}x\left(50-x\right)\)
\(\Rightarrow x^2-50x+600=0\Rightarrow\left[{}\begin{matrix}x=20\left(loại\right)\\x=30\end{matrix}\right.\)
Vậy chiều rộng mảnh đất là 20 (m)

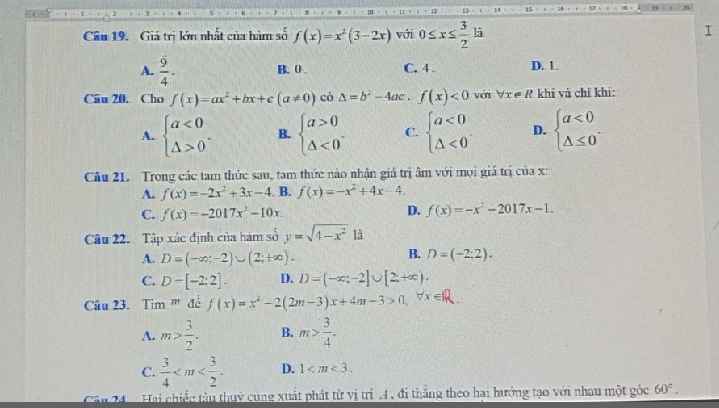
19.
\(f\left(x\right)=x^2\left(3-2x\right)=x.x.\left(3-2x\right)\le\left(\dfrac{x+x+3-2x}{3}\right)^3=1\)
\(\Rightarrow\max\limits_{\left[0;\dfrac{3}{2}\right]}f\left(x\right)=1\)
20.
\(f\left(x\right)< 0;\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
21.
A là đáp án đúng, do đa thức \(f\left(x\right)=-2x^2+3x-4\) có:
\(\left\{{}\begin{matrix}a=-2< 0\\\Delta=3^2-4.\left(-2\right).\left(-4\right)=-23< 0\end{matrix}\right.\)
22.
ĐKXĐ: \(4-x^2\le0\Rightarrow\left(2-x\right)\left(2+x\right)\le0\)
\(\Rightarrow-2\le x\le2\Rightarrow D=\left[-2;2\right]\)
23.
\(f\left(x\right)>0;\forall x\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(2m-3\right)^2-\left(4m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-16m+12< 0\)
\(\Rightarrow1< m< 3\)



Ta có \(\widehat{S}+\widehat{SGQ}+\widehat{Q}=180^0\Rightarrow\widehat{S}+\widehat{Q}=180^0-\widehat{SGQ}\)
Mà \(\widehat{S}-\widehat{Q}=12^0\Rightarrow\left\{{}\begin{matrix}\widehat{S}=\dfrac{180^0-\widehat{SGQ}+12^0}{2}=96^0-\dfrac{\widehat{SGQ}}{2}\\\widehat{Q}=\dfrac{180^0-\widehat{SGQ}-12^0}{2}=84^0-\dfrac{\widehat{SGQ}}{2}\end{matrix}\right.\)
Mà GP là p/g nên \(\widehat{QGP}=\widehat{PGS}=\dfrac{\widehat{SGQ}}{2}\)
\(\Rightarrow\widehat{Q}=84^0-\widehat{QGP}\)
Ta có \(\widehat{GPS}=\widehat{Q}+\widehat{QGP}=84^0-\widehat{QGP}+\widehat{QGP}=84^0\) (tc góc ngoài)

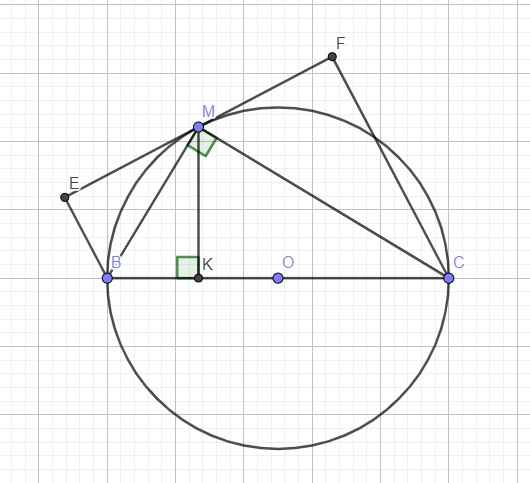
\(\widehat{BME}=\widehat{BMK}\) (do K đối xứng E qua MB)
Mà \(\widehat{BMK}=\widehat{BCM}\) (cùng phụ \(\widehat{MBC}\))
\(\Rightarrow\widehat{BME}=\widehat{BCM}\)
\(\Rightarrow ME\) là tiếp tuyến của (O) tại M
Tương tự, ta có MF là tiếp tuyến của (O) tại M
\(\Rightarrow M;E;F\) thẳng hàng
\(\Rightarrow S_{BEFC}=S_{BEMK}+S_{CFMK}=2S_{BMK}+2S_{CMK}=2S_{MBC}\)
Mà \(S_{MBC}=\dfrac{1}{2}MK.BC\Rightarrow S_{MBC-max}\) khi \(MK_{max}\)
\(\Rightarrow M\) nằm chính giữa cung BC \(\Rightarrow MK_{max}=R=4\left(cm\right)\)
\(\Rightarrow S_{BEFC-max}=2.\dfrac{1}{2}.4.8=32\left(cm^2\right)\)

để A là số nguyên thì \(x-9-5⋮\sqrt{x}+3\)
\(\Leftrightarrow\sqrt{x}+3\inƯ\left(5\right)\)
\(\Leftrightarrow\sqrt{x}+3=5\)
hay x=4

TH1: \(x=14\Rightarrow A=0\) (thỏa mãn)
TH2: \(x\ne14\Rightarrow A\) nguyên khi \(x\) là SCP và \(\dfrac{x-14}{\sqrt{x}+3}\in Z\Rightarrow\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-5}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\sqrt{x}-3-\dfrac{5}{\sqrt{x}+3}\in Z\)
\(\Rightarrow\dfrac{5}{\sqrt{x}+3}\in Z\Rightarrow\sqrt{x}+3=Ư\left(5\right)=5\) (do \(\sqrt{x}+3\ge3\))
\(\Rightarrow x=4\)
Vậy \(x=\left\{4;14\right\}\) có 2 giá trị

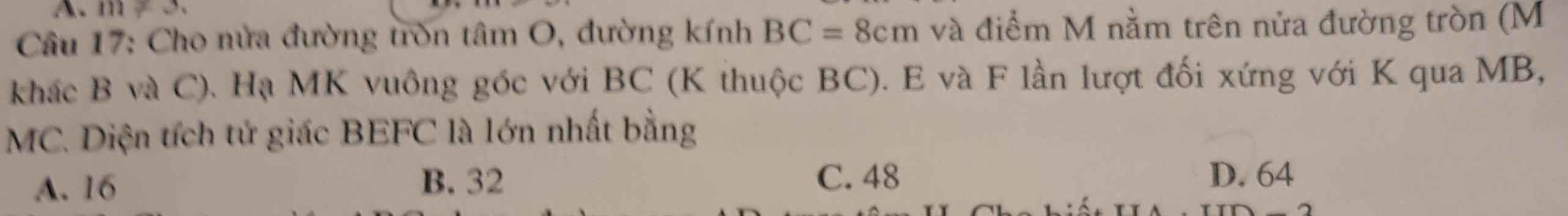


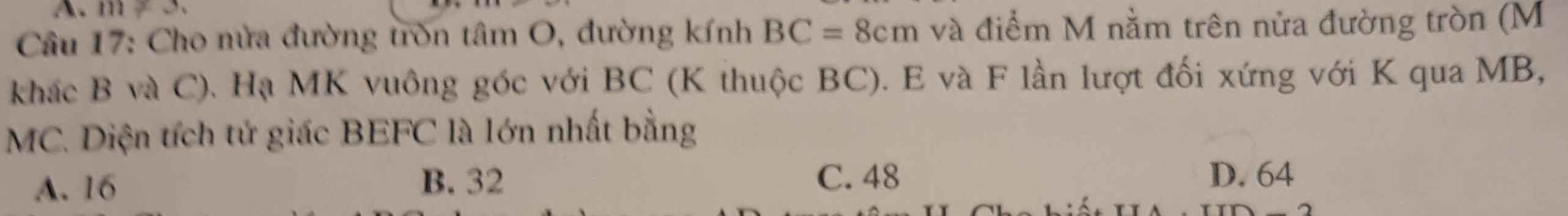
Gọi AB là dây cung qua M, H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH\le OM=3\)
Áp dụng định lý Pitago:
\(OH^2+AH^2=OA^2=25\)
\(\Rightarrow AB=2AH=2\sqrt{25-OH^2}\)
AB nguyên khi \(25-OH^2=\dfrac{k^2}{4}\)
\(\Rightarrow OH^2=25-\dfrac{k^2}{4}\)
\(0\le OH\le3\Rightarrow0\le OH^2\le9\)
\(\Rightarrow0\le25-\dfrac{k^2}{4}\le9\)
\(\Rightarrow64\le k^2\le100\Rightarrow8\le k\le10\)
\(\Rightarrow k=\left\{8;9;10\right\}\) có 3 giá trị nguyên