Trình bày cách giải giúp em với ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KB
8 tháng 4 2022
2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
KB
8 tháng 4 2022
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...
NL
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Câu 10 sai, đáp án B đúng, sử dụng đan dấu trên trục số dễ dàng thấy:
12. Câu này sai, A mới đúng. Đơn giản là em nhìn kĩ lại công thức lượng giác là thấy thôi, nhầm lẫn về hệ số trong công thức biến tích thành tổng
\(cosa.cosb=\dfrac{1}{2}....\)
14. Đáp án C đúng
\(\overrightarrow{BA}=\left(2;2\right)=2\left(1;1\right)\) nên trung trực AB nhận (1;1) là 1 vtpt
Gọi M là trung điểm AB \(\Rightarrow M\left(0;2\right)\)
Phương trình: \(1\left(x-0\right)+1\left(y-2\right)=0\Leftrightarrow x+y-2=0\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2021
Câu 1-7 đúng
Câu 8 sai, \(2-x\ge0\Rightarrow x\le2\)
Câu 9 đến 12 đúng, 13 sai: \(\overrightarrow{AB}=\left(2;-2\right)\Rightarrow AB=\sqrt{2^2+\left(-2\right)^2}=2\sqrt{2}\)
\(R=\dfrac{AB}{2}=\sqrt{2}\)
Câu 14 sai: \(\left|x-1\right|\le1\Leftrightarrow\left\{{}\begin{matrix}x-1\ge-1\\x-1\le1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\le2\end{matrix}\right.\) \(\Leftrightarrow x\in\left[0;2\right]\)
Câu 15 đúng. Phần còn lại hôm qua đã làm rồi
H9
HT.Phong (9A5)
CTVHS
23 tháng 2 2023
Câu 32: \(CH_4+2O_2\xrightarrow[]{t^o}CO_2+2H_2O\)
\(0,25\) \(\rightarrow0,25mol\)
\(V_{CO_2}=0,25.22,4=5,6\left(l\right)\)
Chọn A
Câu 34:
\(C_2H_4+3O_2\rightarrow2H_2O+2CO_2\)
\(n_{C_2H_4}=\dfrac{14}{28}=0,5\left(mol\right)\)
Theo PT ta có:
\(n_{CO_2}=2n_{C_2H_4}=2.0,5=1\left(mol\right)\)
\(\Rightarrow m_{CO_2}=1.44=44\left(g\right)\)
Chọn A
Câu 38: Thể tích tối đa của khí CO2 thu được ở đktc là:
\(n_{CO_2}=\dfrac{m}{M}=\dfrac{1,2}{12}=0,1\left(mol\right)\)
\(V_{CO_2}=22,4.0,1=2,24\left(l\right)\)
Chọn D
7 tháng 5 2022
- Cho Cu(OH)2 vào 2 dung dịch:
+ Không hiện tượng: C2H5OH
+ Chất rắn tan, tạo thành dd màu xanh: C2H4(OH)2
\(2C_2H_4\left(OH\right)_2+Cu\left(OH\right)_2\rightarrow\left[C_2H_4\left(OH\right)O\right]_2Cu+2H_2O\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
12 sai, C mới là đáp án đúng
13 sai, A đúng, \(sin-sin=2cos...sin...\)
18.
\(\Leftrightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=m^2-m\left(-m+3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m^2-3m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< \dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow m=1\)
Đáp án B
22.
Để pt có 2 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1< m< 3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2\left(2m-3\right)}{m-2}\\x_1x_2=\dfrac{5m-6}{m-2}\end{matrix}\right.\)
\(\dfrac{-2\left(2m-3\right)}{m-2}+\dfrac{5m-6}{m-2}\le0\)
\(\Leftrightarrow\dfrac{m}{m-2}\le0\) \(\Leftrightarrow0\le m< 2\)
Kết hợp điều kiện delta \(\Rightarrow1< m< 2\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
24.
Đề bài câu này dính lỗi, ko có điểm M nào cả, chắc là đường thẳng đi qua A
Đường tròn (C) tâm I(1;-2) bán kính R=4
\(\overrightarrow{IA}=\left(1;3\right)\)
Gọi d là đường thẳng qua A và cắt (C) tại 2 điểm B và C. Gọi H là trung điểm BC
\(\Rightarrow IH\perp BC\Rightarrow IH=d\left(I;d\right)\)
Theo định lý đường xiên - đường vuông góc ta luôn có: \(IH\le IA\)
Áp dụng Pitago cho tam giác vuông IBH:
\(BH=\sqrt{IB^2-IH^2}\Leftrightarrow\dfrac{BC}{2}=\sqrt{16-IH^2}\)
\(\Rightarrow BC_{min}\) khi \(IH_{max}\Leftrightarrow IH=IA\)
\(\Leftrightarrow IA\perp d\Rightarrow d\) nhận \(\overrightarrow{IA}\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)
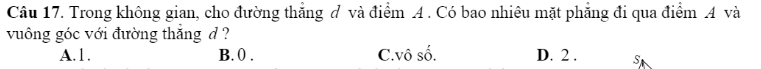
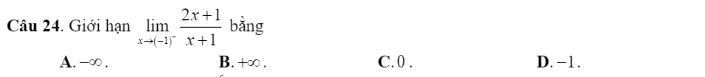
Chóp S.ABCD đều nên ABCD là HV \(\Rightarrow BD\perp AC\) (1)
O = \(AC\cap BD\) . Dễ dàng c/m : BD \(\perp SO\) (2)
Từ (1) ; (2) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SA\) \(\Rightarrow\left(SA;BD\right)=90^o\)
Chọn D