cứu em đi mn=(((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


REFER
Câu tục ngữ "Có chí thì nên" nghe có vẻ ngắn gọn và đơn giản nhưng ẩn chứa một tầng ý nghĩa thật lớn lao. “Chí” có thể hiểu là sự quyết tâm, nghị lực, hoài bão, lý tưởng khi thực hiện một kế hoạch hay làm một điều gì đó. “Có chí thì nên”, “nên” ở đây tức là đạt được thành công, đạt được kết quả như mong muốn, như đã đặt ra. Như vậy, cùng với cách nói “Có ..thì”, như một lời khẳng định đanh thép, ông cha ta đã đặt ra vài trò của ý chí, nghị lực trong cuộc sống, cụ thể là trên con đường thành công của mỗi người. Con người ta cần có sự kiên trì, quyết tâm, lý tưởng thì mọi khó khăn, gian nan, thử thách, thất bại đều sẽ có thể vượt qua và đạt được kết quả như mong ước.
Tham khảo:
Con người không thể thiếu đức tính kiên trì và ý chí nghị lực nếu muốn thành công trong cuộc sống. Câu tục ngữ “Có chí thì nên” mà ông cha ta truyền lại đã khẳng định điều đó. “Chí” là hoài bão, lý tưởng tốt đẹp, là ý chí, nghị lực và sự kiên trì. “Nên” là sự thành công trong mọi việc. “Có chí thì nên” khẳng định vai trò và ý nghĩa to lớn của ý chí trong cuộc sống. Khi ta làm bất cứ việc gì, nếu có ý chí, nghị lực và sự kiên trì thì chúng ta sẽ vượt qua được mọi khó khăn, trở ngại để đi đến thành công bởi vì tất cả những thành công đều phải trải qua quá trình rèn luyện lâu dài. Tính kiên trì sẽ giúp chúng ta không nản chí trước những thất bại và biết rút kinh nghiệm từ những thất bại đó để làm nên thành công sau này. Nếu chỉ có một lần thất bại đã nản lòng, nhụt chí thì chúng ta sẽ không bao giờ đạt được mục tiêu của mình. Tóm lại, mỗi học sinh nên hiểu được lợi ích của đức tính kiên trì và bắt đầu rèn luyện ý chí, nghị lực ngay từ những việc nhỏ trong học tập để sau này trở thành những người có ích cho xã hội.


a: Trong mp(SBC), gọi M là giao điểm của SO với BC
Chọn mp(SBC) có chứa SO
\(SO\subset\left(SBC\right);SO\subset\left(SAO\right)\)
Do đó: (SBC) giao (SAO)=SO
Vì M là giao điểm của CB với SO
nên M là giao điểm của CB với mp(SAO)
b: Gọi N là giao điểm của AC và BD
\(N\in AC\subset\left(SAC\right)\)
\(N\in BD\subset\left(SBD\right)\)
Do đó: \(N\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SN
c: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
d: AB//CD
CD\(\subset\)(SCD)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)

a: Xét ΔABE và ΔHBE có
BA=BH
\(\widehat{ABE}=\widehat{HBE}\)
BE chung
Do đó: ΔABE=ΔHBE
b: Ta có: ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
d: ta có: EA=EH
mà EH<EC
nên EA<EC


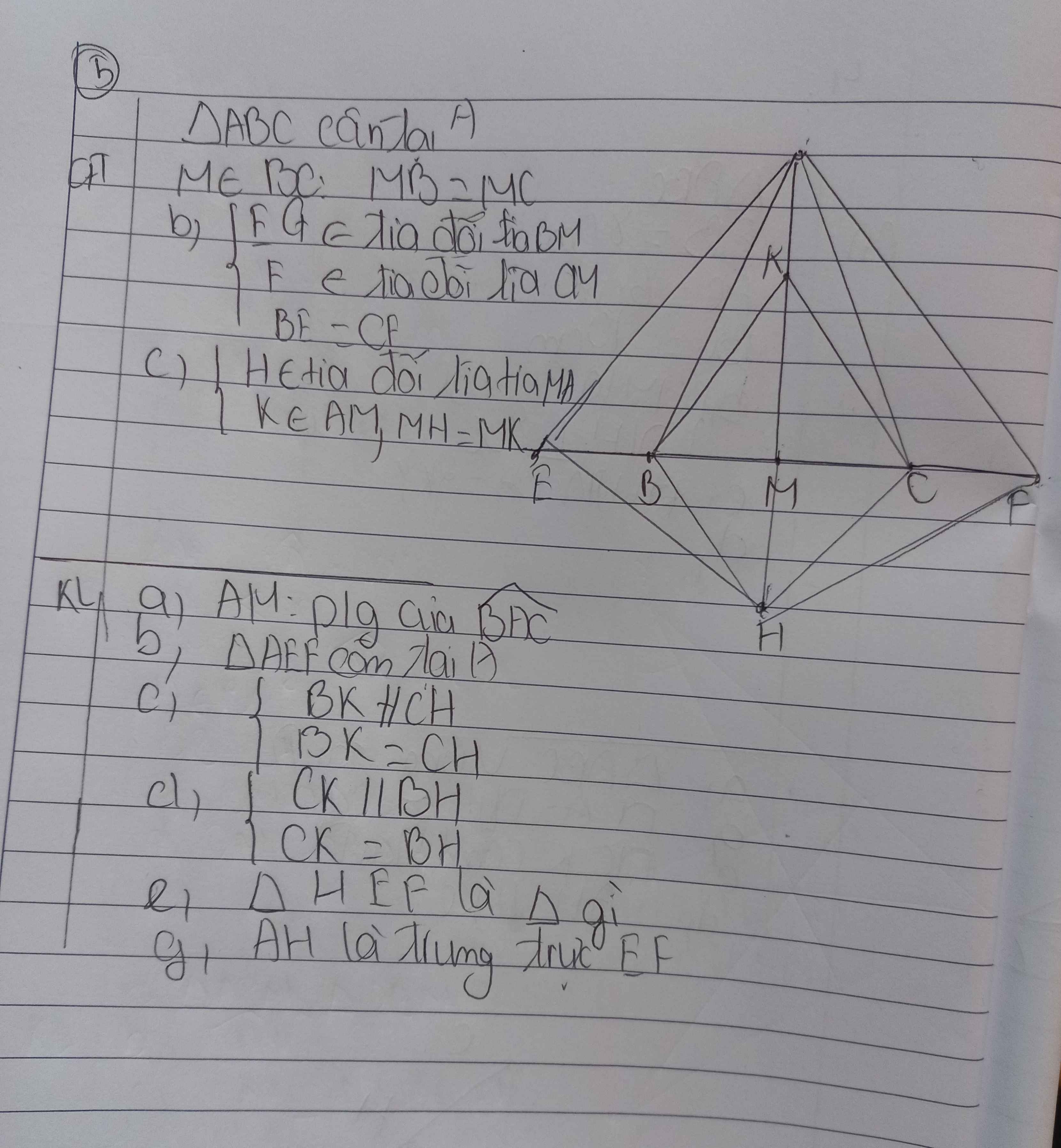
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Xét ΔABE và ΔACF có
AB=AC
\(\widehat{ABE}=\widehat{ACF}\)
BE=CF
Do đó: ΔABE=ΔACF
c: Xét tứ giác BKCH có
M là trung điểm của BC
M là trung điểm của HK
Do đó: BKCH là hình bình hành
Suy ra: BK//CH; BK=CH
d: Ta có: BKCH là hình bình hành
nên CK//BH; CK=BH

\(a,\) Ta có :
\(OB=OC=R\)
\(AB=AC\) (t/c 2 tiếp tuyến cắt nhau)
\(\Rightarrow OA\) là đường trung trực của \(BC\)
\(\Rightarrow OA\perp BC\)
\(b,\) Xét \(\Delta ABE\) và \(\Delta ABD\) có :
\(\widehat{BAE}\) chung
\(\widehat{BED}=\widehat{ABD}\) (cùng chắn \(\stackrel\frown{BD}\) )
\(\Rightarrow\Delta ABE\sim\Delta ABD\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{AE}{AB}\)
\(\Rightarrow AB^2=AD.AE\)
Xét \(\Delta OAB\perp\) tại \(A\) có :
\(AB^2=AH.AO\left(HTL\right)\) \(\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\) \(AD.AE=AH.AO\)
Xét \(\Delta AHD\) và \(\Delta AEO\) có :
\(\widehat{OAE}chung\)
\(\dfrac{AD}{AH}=\dfrac{AO}{AE}\left(AD.AE=AH.AO\right)\)
\(\Rightarrow\Delta AHD\sim\Delta AEO\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{AEO}\)
\(\Rightarrow\) Tứ giác \(DHOE\) nội tiếp (góc ngoài = góc đối trong)





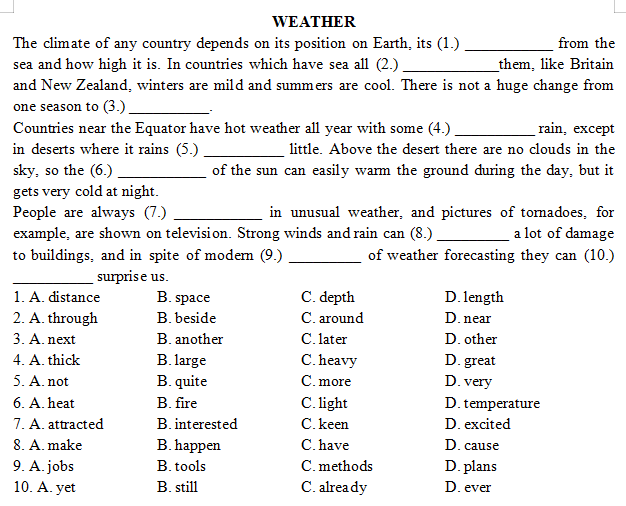



Câu 9:
Các dấu phảy trong câu sau có tác dụng ngăn cách bộ phận cùng làm vị ngữ và ngăn cách các vế trong câu ghép.
Câu 10:
Bằng cách lặp từ ngữ không gian