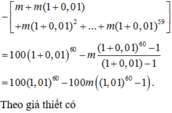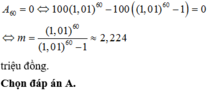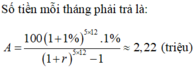Ông Ba vay ngân hàng 500 triệu với lãi suất là x/100. hết năm thứ nhát ngân hàng cho vay tiếp với số tiền ông phải trả gồm cả 500 triệu công với tiền lời một năm của 500 tiệu. Ngân hàng vẫn cho vay với lãi suất không đỗi , Sau hai năm ông Ba phải trả ngân hàng với số tiền là 605 triệu .Hỏi lãi suất ngân hàng đã cho vay là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 6 2023
A, Số tiền lãi ông Ba nhận được là:
\(200\times0,5:100=1\)(triệu đồng)
B, Số tiền lãi của ngân hàng là:
\(100\times0,6:100=0,6\)(triệu đồng)
Số tiền ông Ba nhận lại là:
\(1-0,6=0,4\)(triệu đồng)
Đáp số: 0,4 triệu đồng
4 tháng 1
A, Số tiền lãi ông Ba nhận được là:
(triệu đồng)
B, Số tiền lãi của ngân hàng là:
(triệu đồng)
Số tiền ông Ba nhận lại là:
(triệu đồng)
Đáp số: 0,4 triệu đồng
CM
29 tháng 7 2019
Đáp án B
Áp dụng CT trả góp ta có m = 100 1 + 12 % 12 12 12 % 12 1 + 12 % 12 12 − 1 ≈ 0 , 885 triệu đồng
G
18 tháng 10 2016
Đây là câu 21 của đề minh họa thị THPT QG 2017.
Lãi suất 12%/năm => lãi suất 1%/tháng.
Nếu còn nợ a đồng thì phải trả lãi 0,01 a cho 1 tháng.
Sau tháng đầu tiên, sau khi trả m đồng thì ông A còn nợ là:
(a + 0,01.a) - m = a. 1,01 - m
Sau tháng thứ hai, sau khi trả tiếp m đồng thì ông A còn nợ là:
(a . 1,01 - m) . 1,01 - m
Sau tháng thứ ba, sau khi trả tiếp m đồng thì ông A còn nợ là:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m
Con số nợ cuối cùng này phải bằng 0, suy ra:
[(a. 1,01 - m) . 1,01 - m] . 1,01 - m = 0
=> \(m=\frac{a.1,01^3}{1,01^2+1,01+1}=\frac{a.1,01^3\left(1,01-1\right)}{1,01^3-1}=\frac{a.1,01^3.0,01}{1,01^3-1}\)
Thay a = 100 vào ta có:
\(m=\frac{1,01^3}{1,01^3-1}\)