Có thể giải chi tiết hộ mình được không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bn vào những câu hỏi tương tự nhé,trong do sẽ có câu trả lời

gọi số cần tìm là x
ta có :
\(x-\left(\frac{x-6}{10}\right)=4461\text{ hay ta có }\frac{9}{10}\times x=\frac{22302}{5}\)
Vậy ta có \(x=\frac{22302}{5}:\frac{9}{10}=4956\)
Vậy số cần tìm là 4956

Điểm A nằm giữa hai điểm B và C
Bạn xem ghi nhớ trong SGK
Sẽ làm được thôi

a = 2002 x 2002 = ( 2000 + 2 ) x 2002
= 2000 x 2002 + 2 x 2002
b = 2000 x 2004 = 2000 x ( 2002 + 2 )
= 2000x 2002 + 2 x 2000
ta thấy 2000 x 2002 + 2 x 2002 > 2000 x 2002 + 2 x 2000 nên a > b
a=2002x2002
a=(2000+2)x2002
a=2000x2002+2x2002
a=2000x2002+2x(2000+2)
a=2000x2002+2x2000+4
a=2000x(2002+2)+4
a=2000x2004+4
a=b+4
Vậy a lớn hơn b và lớn hơn 4 đơn vị.

Nếu: \(x-1\ge0\) \(\Leftrightarrow\)\(x\ge1\) thì: \(\left|x-1\right|=x-1\)
Khi đó ta có: \(x^2-3x+2+x-1=0\)
\(\Leftrightarrow\) \(\left(x-1\right)^2=0\)
\(\Leftrightarrow\) \(x-1=0\)
\(\Leftrightarrow\) \(x=1\) (thỏa mãn)
Nếu \(x-1< 0\)\(\Leftrightarrow\)\(x< 1\) thì \(\left|x-1\right|=1-x\)
Khi đó ta có: \(x^2-3x+2+1-x=0\)
\(\Leftrightarrow\) \(x^2-4x+3=0\)
\(\Leftrightarrow\) \(\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\) \(\orbr{\begin{cases}x-1=0\\x-3=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1\\x=3\end{cases}}\) (không thỏa mãn)
Vậy....
Lập bảng xét dấu :
| x | 1 | ||
| x-1 | - | 0 | + |
+) Nếu \(x\ge1\Leftrightarrow|x-1|=x-1\)
\(pt\Leftrightarrow x^2-3x+2+\left(x-1\right)=0\)
\(\Leftrightarrow x^2-3x+2+x-1=0\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\left(tm\right)\)
+) Nếu \(x< 1\Leftrightarrow|x-1|=1-x\)
\(pt\Leftrightarrow x^2-3x+2+\left(1-x\right)=0\)
\(\Leftrightarrow x^2-3x+2+1-x=0\)
\(\Leftrightarrow x^2-4x+3=0\)
\(\Leftrightarrow\left(x^2-4x+4\right)-1=0\)
\(\Leftrightarrow\left(x-2\right)^2=1\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=-\sqrt{1}\\x-2=\sqrt{1}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x-2=-1\\x-2=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=3\end{cases}}\) ( loại )
Vậy phương trình có tập nghiệm \(S=\left\{1\right\}\)

ặc :v
\(\Leftrightarrow\frac{1}{1+x^2}-\frac{1}{1+xy}+\frac{1}{1+y^2}-\frac{1}{1+xy}\ge0\)
\(\Leftrightarrow\frac{1+xy-1-x^2}{\left(1+x^2\right)\left(1+xy\right)}+\frac{1+xy-1-y^2}{\left(1+y^2\right)\left(1+xy\right)}\ge0\)
\(\Leftrightarrow\frac{x\left(y-x\right)\left(1+y^2\right)}{\left(1+x^2\right)\left(1+y^2\right)\left(1+xy\right)}+\frac{y\left(x-y\right)\left(1+x^2\right)}{\left(1+y^2\right)\left(1+xy\right)}\ge0\)
\(\Leftrightarrow\frac{x\left(y-x\right)\left(1+y^2\right)+y\left(x-y\right)\left(1+x^2\right)}{\left(1+x^2\right)\left(1+y^2\right)\left(1+xy\right)}\ge0\)
\(\Leftrightarrow\frac{\left(x-y\right)^2\left(xy-1\right)}{\left(1+x^2\right)\left(1+y^2\right)\left(1+xy\right)}\ge0\)
Ok chưa :v

Gọi x, y lần lượt là số điện trở của R1 và R2.
Vì đoạn mạch mắc nối tiếp nên ta có: Rtđ = R1 + R2 + ... + Rn
từ đó ta có: 4x + 8y = 48
⇔ x + 2y = 12
⇒ x = 12 - 2y
| y | x = 12 - 2y |
| 0 | 12 |
| 1 | 10 |
| 2 | 8 |
| 3 | 6 |
| 4 | 4 |
| 5 | 2 |
| 6 | 0 |
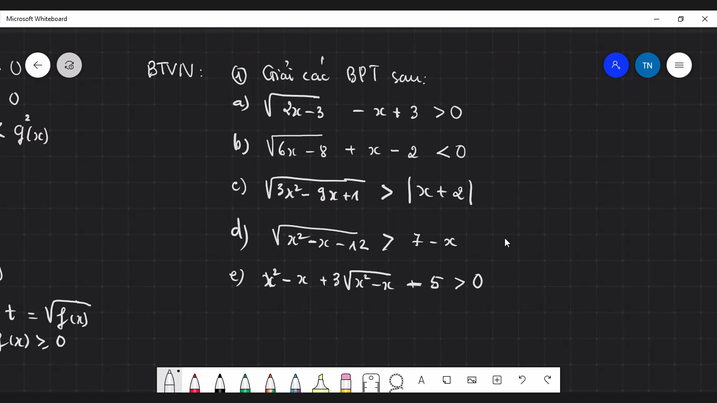
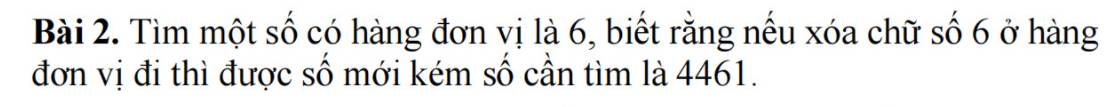
Em cần hỗ trợ như nào vậy em?
1.
Nếu BC là đáy lớn \(\Rightarrow S_{MBC}=S_{MAB}+S_{ABCD}\Rightarrow S_{MBC}>S_{ABCD}\) (không thỏa mãn)
\(\Rightarrow BC\) là đáy nhỏ \(\Rightarrow S_{MAD}=S_{MBC}+S_{ABCD}=S_{MBC}+3S_{MBC}=4S_{MBC}\)
Từ M kẻ đường thẳng vuông góc AD và BC, lần lượt cắt BC tại H và AD tại K
\(\Rightarrow S_{MAD}=\dfrac{1}{2}MK.AD\) ; \(S_{MBC}=\dfrac{1}{2}MH.BC\)
\(\Rightarrow MK.AD=4MH.BC\Rightarrow\dfrac{AD}{BC}=4.\dfrac{MH}{KM}=4.\dfrac{AM}{BM}=4.\dfrac{BC}{AD}\) (theo Talet)
\(\Rightarrow AD^2=4BC^2\Rightarrow AD=2BC\Rightarrow\overrightarrow{AD}=2\overrightarrow{BC}\)
Ta có: \(\overrightarrow{BC}=\left(7;-1\right)\) ; \(\overrightarrow{AD}=\left(x_0+2;y_0+2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_0+2=14\\y_0+2=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=12\\y_0=-4\end{matrix}\right.\) \(\Rightarrow x_0-y_0=16\)