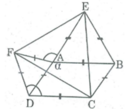
Cho hình bình hành ABCD có góc A tù. Ở phía ngoài hình bình hành ta vẽ các tam giác đều ADF, ABE.
a) Tính góc EAF; góc AEF
b) Chứng minh rằng: Tam giác CEF đều.
Giải từng bước giúp mình nhé ! Mơn nhìu!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 6 2017
Vì ∠ (BAD) + ∠ (BAE) + ∠ (EAF) + ∠ (FAD) = 360 0
⇒ ∠ (EAF) = 360 0 – ( ∠ (BAD) + ∠ (BAE) + ∠ (FAD) )
Mà ∠ (BAD) = α 2 (gt)
∠ (BAE) = 60 0 (ΔBAE đều)
∠ (FAD) = 60 0 (ΔFAD đều)
Nên ∠ (EAF) = 360 0 – ( α 2 + 60 0 + 60 0 ) = 240 0 – α
22 tháng 3 2020
Bạn tự vẽ hình nhé!
Giải
a) Ta có:
\(\widehat{EAF}+\widehat{EAB}+\widehat{BAD}+\widehat{DAF}=360^0\)
\(\Rightarrow\widehat{EAF}+60^0+60^0+110^0=360^0\)
\(\Rightarrow\widehat{EAF}=130^o\)
b) Vì ABCD là hình bình hành nên:
\(\widehat{BAD}+\widehat{ADC}=180^o\)
\(110^o+\widehat{ADC}=180^o\)
\(\Rightarrow\widehat{ADC}=70^o\)
\(\Rightarrow\widehat{CDF}=\widehat{ADC}+\widehat{ADF}=70^o+60^o=130^o\)
Xét \(\Delta\)EAF và \(\Delta\)CDF có:\(\hept{\begin{cases}AE=DC\left(=AB\right)\\AF=DF\\\widehat{EAF}=\widehat{CDF}=130^o\end{cases}\Rightarrow\Delta EAF=\Delta CDF\left(cgc\right)}\)
c) Ta có: \(\Delta EAF=\Delta CDF\left(cmt\right)\Rightarrow EF=CF\)
Tương tự cũng có: \(\Delta CDF=\Delta EBC\left(cgc\right)\Rightarrow CF=EC\)
\(\Rightarrow\Delta\)EFC là tam giác đều (đpcm)
26 tháng 8 2016
a) Tính góc EAF
EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1)
b) Chứng minh rằng tam giác CEF là tam giác đều
ABC^ = ADC^ = 180* - a
=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2)
CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3)
AF = DF = AD = BC (4)
CD = AB = BE = AE (5)
(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c)
=> CF = CE = EF => CEF là tam giác đều
TT
20 tháng 11 2018
a,tính góc EAF
EAF^=360* - ( DAF^+BAD^+BAE^)=360*-(60*+a+60*)=240*-a(1)
b,chứng minh rằng tam giác CÈ là tam giác đều
ABC^=ADC^+ADF^=180*-a+60*=240*-a(2)
CBE^=ABC^+ABE^=180*-a+60*=240*-a(3)
AF=DF=AD=BC(4)
CD=AB=BE=AE(5)
(1) (2) (3) (4) và (5) => tam giác CDF=tam giác EAF (c.g.c)
=> CF=CE=EF=>CÈ là tam giác đều
10 tháng 9 2017
Tính góc EAF
EAF^ = 360* - (DAF^ + BAD^ + BAE^) = 360* - (60* + a + 60*) = 240* - a (1)
b) Chứng minh rằng tam giác CEF là tam giác đều
ABC^ = ADC^ = 180* - a
=> CDF^ = ADC^ + ADF^ = 180* - a + 60* = 240* - a (2)
CBE^ = ABC^ + ABE^ = 180* - a + 60* = 240* - a (3)
AF = DF = AD = BC (4)
CD = AB = BE = AE (5)
(1) (2) (3) (4) và (5) => Δ CDF = ΔEBC = Δ EAF ( c.g.c)
=> CF = CE = EF => CEF là tam giác đều
KT
10 tháng 5 2018
\(\widehat{ABE}=\widehat{ABC}+\widehat{CBE}=\widehat{ABC}+60^0\) (do tam giác BCE đều)
\(\widehat{FDA}=\widehat{ADC}+\widehat{CDF}=\widehat{ADC}+60^0\) (do tam giác DFC đều)
ABCD là hình bình hành => \(\widehat{ABC}=\widehat{AD}C\)
suy ra: \(\widehat{ABE}=\widehat{FDA}\)
Xét \(\Delta ABE\)và \(\Delta FDA\)có:
\(AB=FD\) (cùng bằng DC)
\(\widehat{ABE}=\widehat{FDA}\) (cmt)
\(BE=DA\) (cùng bằng BC)
suy ra: \(\Delta ABE=\Delta FDA\) (c.g.c)
\(\Rightarrow\)\(AE=AF\) (1)
Ta có: \(\widehat{FCE}=360^0-\widehat{DCF}-\widehat{BCE}-\widehat{BCD}\)
\(=360^0-60^0-60^0-\widehat{BCD}\)
\(=240^0-\widehat{BCD}\)
\(=240^0-\left(180^0-\widehat{ABC}\right)=60^0+\widehat{ABC}\)
suy ra: \(\widehat{FCE}=\widehat{ABE}\)
dễ dàng c/m: \(\Delta ABE=\Delta FCE\) (c.g.c)
\(\Rightarrow\)\(AE=FE\) (2)
Từ (1) và (2) suy ra: \(AF=FE=EA\)
hay \(\Delta AEF\)đều
\(\Rightarrow\)\(\widehat{EAF}=60^0\)
